8+2=10м - от столба до конца тени
согласно подобию треугольников
2/1,5=10/х
х=1,5*10/2=7,5м - высота, на которой подвешен фонарь
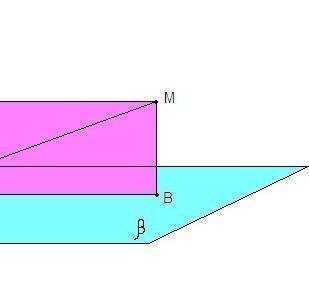
α⊥β, α∩β = а.
Проведем МА⊥α и МВ⊥β.
Тогда МА = 12 см - расстояние от точки М до плоскости α,
МВ = 5 см - расстояние от точки М до плоскости β.
Затем проведем АС⊥а и ВС⊥а.
Если прямая, лежащая в одной плоскости, перпендикулярна линии пересечения перпендикулярных плоскостей, то он перпендикулярна другой плоскости. Значит
АС⊥β и ВС⊥α.
АС║МВ и ВС║МА как перпендикуляры к одной плоскости, значит
МАСВ прямоугольник.
Прямая а перпендикулярна плоскости МАВ (а⊥АС и а⊥ВС), значит
а⊥МС.
МС - искомое расстояние от точки М до прямой а.
Из прямоугольного треугольника МАС по теореме Пифагора:
МС = √(МА² + АС²) = √(144 + 25) = √169 = 13 см
столб
|
|
|
| человек
|8м|_2м_
Если провести линию, соединяющую точку, где висит фонарь, с точкой, где кончается тень, то эта линия коснется макушки человека. То есть мы имеем дело с подобными треугольниками: признак подобия по двум углам (фонарь и человек стоят перпендикулярно земле - один угол, второй угол - место схождения нашей воображаемой линии и линии тени).
Коэффициент подобия k=2/(8+2)=0,2
1,5:0,2=7,5 (м) - искомая высота
ответ: фонарь закреплён на высоте 7,5 метров.