Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Осноположником геометрии можно считать Евклида. В начале XX века великий французский архитектор Ле Корбюзье сказал: «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». В развитии Геометрия можно указать четыре основных периода, переходы между которыми обозначали качественное изменение Геометрии.
Первый — период зарождения Геометрии как математической науки — протекал в Древнем Египте, Вавилоне и Греции примерно до 5 в. до н. э. Первичные геометрические сведения появляются на самых ранних ступенях развития общества. Зачатками науки следует считать установление первых общих закономерностей, в данном случае — зависимостей между геометрическими величинами. Этот момент не может быть датирован. Самое раннее сочинение, содержащее зачатки Геометрия, дошло до нас из Древнего Египта и относится примерно к 17 в. до н. э., но и оно, несомненно, не первое. Геометрические сведения того периода были немногочисленны и сводились прежде всего к вычислению некоторых площадей и объёмов. Они излагались в виде правил, по-видимому, в большой мере эмпирического происхождения, логические же доказательства были, вероятно, ещё очень примитивными. Геометрия, по свидетельству греческих историков, была перенесена в Грецию из Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве.Геоме́трия (от др. ... γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.
1.180°-149°= 31°.
7. - (нет картинок, ничего не понятно, если добавишь позже, я отвечу)
8. -
9. -
10. АС= 37+10=47см, ВС= 47-5 =42 см; Р = АВ + АС + ВС = 37+42+47 = 126 см.
11. АВ = Р - ВС - АС = 60-26-15 = 19 см.
12.АС = 35+6 = 41 см, ВС = 41-9 = 32 см, Р = 35+32+41 см
13. ВС = 2ВЕ, т.к. АЕ медиана => ВС = 34,1×2 = 68,2 см.
14. ЕС =
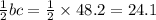
15. ЕС =
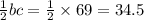
16.Рассмотрим ∆AMB, ∠ВАМ +∠АВМ = 180-120= 60°; Из точек А и В проведены биссектрисы => ∠А+В = 60 ×2 = 120°
17.∠В = 180-87-26 = 67°
18. Т.к. ∆АВС равнобедренный, ∠В=∠С => ∠А = 180 - (65+65) = 50°
19. Т.к. ∆АВС равнобедренный, ∠А=∠С; т.к. АD биссектриса, ∠DAC= 1/2 ∠A; Пусть ∠DAC - x, тогда ∠С= 2х, составим уравнение:
2х+х+105=180
3х=75
х=25 => ∠С=2×25 = 50°
20. ∠А= 180-51-53= 76°
Объяснение:
Объяснения написаны вместе с ответами :)
по теореме Пифагора найдем высоту
BH(2)=625-225=400
BH=20
проведем высоту CE
CE=BH=20
найдем ED
так же по теореме Пифагора
ED(2)=841-400=441
ED=21
AD=15+33+21=69