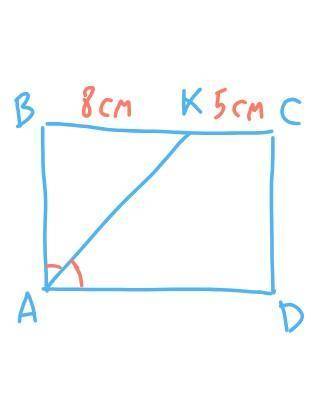
Периметр прямоугольника равен удвоенной сумме двух его смежных сторон. P = 2(AB+BC),
BC = BK + KC = 8 см + 5 см = 13 см.
AK — биссектрисса угла A, угол BAK = угол KAD = 90°÷2 = 45°,
Рассмотрим треугольник ABK. Сумма углов треугольника равна 180°. угол BKA = 180° – угол ABK – угол BAK = 180° – 90° – 45° = 45°, угол BKA = угол BAK, углы при основании равны, треугольник — равнобедренный, значит боковые стороны равны, AB = BK = 8см.
P = 2(AB + BC) = 2(8см + 13см) = 2 × 21 см = 42 см.
ответ: 42 см
а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен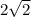 
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,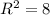 
, 
.
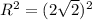
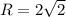в) (5; -7) - центр окружности, R²=16,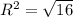 
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
