Question

Медианы, проведенные к катетам прямоугольного треугольника, равны a и b. найти гипотенузу треугольника.

Answer 1

Обозначим катеты через х, у,  а гипотенузу через z. Продлевая медианы на свою длину и для каждой из них достраивая исходные треугольник до параллелограмма, применяем свойство, что в параллелограмме сумма квадратов диагоналей равна сумме квадратов сторон. Получаем систему:
4a²+x²=2z²+2y²
4b²+y²=2z²+2x²
x²+y²=z²
Складываем первое ур-е и второе, и применяем третье:
4a²+4b²+z²=4z²+2z²
4(a²+b²)=5z²
Отсюда $z= 2\sqrt{(a^2+b^2)/5}.$

Answer 2

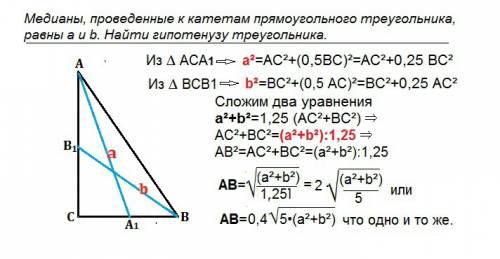
Медианы, проведенные к катетам прямоугольного треугольника, равны a и b. Найти гипотенузу треугольника.

Пусть данный треугольник АВС, угол С=90º, 

а - медиана  АА1 к ВС, b- медиана  ВВ1 к АС. 

В ∆ АСА1 катет СА1=0,5 ВС ⇒ по т.Пифагора:

 а²=АС²+(0,5ВС)²=АС²+0,25 ВС²

В ∆ ВСВ1 катет СВ1=0,5 АС ⇒ по т.Пифагора:

 b²=ВС²+(0,5 АС)²=ВС²+0,25 АС²

Сложим два уравнения 

а²+b²=1,25 (АС²+ВС²)⇒

АС²+ВС²=(а²+b²):1,25 ⇒

АВ²=АС²+ВС²=(а²+b²):1,25 

АВ=√[(а²+b²):1,25]=0,4√[5•(а²+b²)] или 2√[(а²+b²):5], что одно и то же.