Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
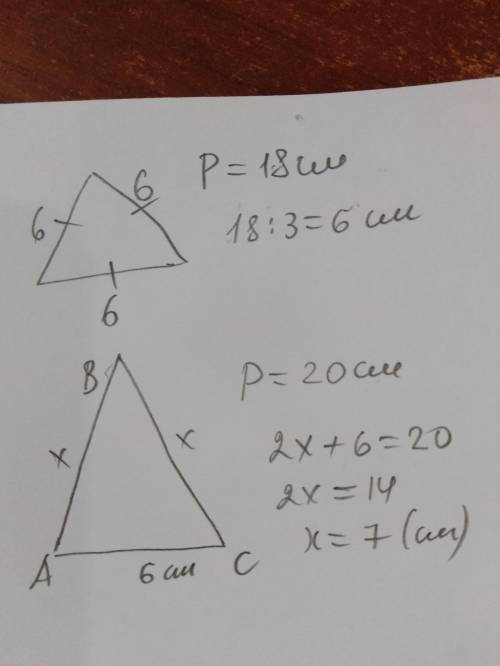
Відповідь:
BD = √3
Пояснення:
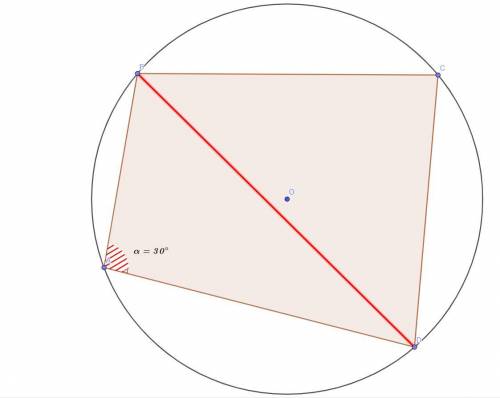
(див. малюнок до задачі)
1) Отож, маємо справу з вписаним чотирикутником. Для початку, давай я просто наведу одну єдину формулу чи то відношення, якою (яким) ми будемо користуватися:
1) a/sinα=b/sinβ=c/sinγ=2R - розширена теорема синусів (див. мал.). Цю Теорему будемо застосовувати до трикутника ABD, де <BAD = 30°.
2) Оскільки діаметр дорівнює подвоєному радіусу, то радіус дорівнює:
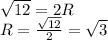 ;
;
3) З трикутника ABD за пропорційністю сторони і протилежних кутів до цієї сторони (тобто за формулою!), маємо, що:
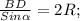
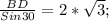
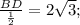
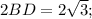
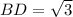 .
.
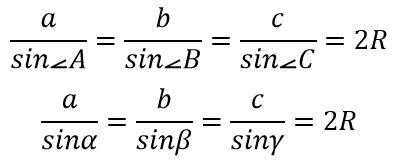
Площадь полной поверхности пирамиды: Sп=Sбок+2Sосн=(Р·l/2)+(2a²√3/4), где Р - периметр основания, l - апофема.
Sп=(3·18·18/2)+(2·18²√3/4)=162(3+√3) см² - это ответ.
Отрезок, соединяющий основания высоты и апофемы, равен радиусу вписанной в основание окружности. Для правильного треугольника r=a√3/6=3√3 см.
Высота пирамиды: h²=l²-r²=18²-(3√3)²=297.
h=3√33 cм.
Объём пирамиды: V=Sh/3=a²h√3/12.
V=18²·3√33·√3/12=243√11 cм³ - это ответ.