Объяснение:
1)Соеденим N и Р .
Рассмотрим ΔNКР. ВС-средняя линия по определению. Значит по т. о средней линии ВС=0,5NР .
Рассмотрим ΔNМР. АД-средняя линия по определению. Значит по т. о средней линии АД=0,5NР .
Поэтому ВС=АД
2) Соеденим М и К.
Рассмотрим ΔМКК. ВАВ-средняя линия по определению. Значит по т. о средней линии АВ=0,5МК .
Рассмотрим ΔМКР. ДС-средняя линия по определению. Значит по т. о средней линии ДС=0,5МК .
Поэтому АВ=ДС.
3) ВС=АД и АВ=ДС, то четырёхугольник АВСД является параллелограммом, т.к. противоположные стороны попарно равны.
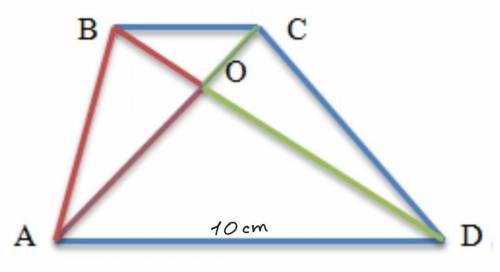
Нужно найти меньшее основание трапеции ABCD — это отрезок ВС.
Решение.
Согласно свойству диагоналей трапеции:
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения - подобны. Значит, ΔAOD~ΔBOC.
По условию Saod = 32 см², Sboc= 8 см².
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Saod / Sboc = k²;
32/8 = k²;
k²= 4;
k= 2 (-2 не подходит).
Коэффициент подобия треугольников AOD и BOC равен 2.
Соответственные стороны этих треугольников относятся и при делении равны коэффициенту.
Т.е. AD / BC = k.
AD=10 см по условию.
10 / ВС = 2;
2ВС=10;
ВС= 5 (см).
ответ: 5 см.
r²=S/π ⇒ r=√(S/π) =√(64/π)=8/√π дм
Sсеч.= 2r·H
2r= 2·8/√π=16/√π
H=S/2r
H= 12√π / (16/√π)=3π/4 = 0,75π(дм)