2). За формулою (ВС+АД)/2=МН, де ВС-менша основа; АД-більша основа, а МН-середня лінія,то АД візьмемо за х, звідси маемо рівняння:
(6+х)/2=11
6+х=22
х=16см.-більша основа АД.
3). х-коєфіціент пропорційності. Звідси АД відноситься до МН, як 5:4, звідси АД=5х, а МН=4х.
Так, як МН більша за ВС на 5см, то МН= 4х+5, а ВС=4х-5см., за формулою (ВС+АД)/2=МН, то маемо рівняння:
(4х-5+5х)/2=4х+5
4х-5+5х=8х+10
9х-8х=15
х=15см.
Звідси ВС=4х-5=4*15-5=55см.; АД=5х=5*15=75см.
Відповідь:55см., 75см.
1).а).так; б).так.
Так, як середня лінія повинна бути меншою за її більшу основу, і більшою за її меншу основу.
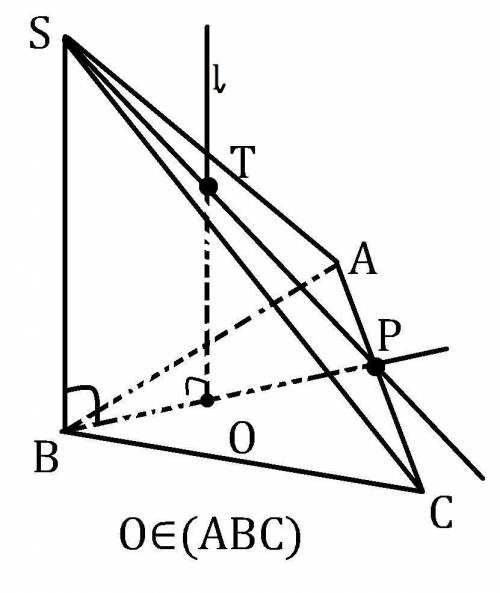
Рисунок к вопросу не был приложен, поэтому возможно пирамида выглядит по другому, но построения нужной точки остаётся правильным.
B,O∈(ABC); BO⊂(ABC); AC⊂(ABC). Пусть BO∩AC=P. *по рисунку O - лежит в треугольнике, поэтому прямые BO и AC не могут быть параллельными, а раз они лежат в одной плоскости, то они пересекаются.
O∈BP⊂(SBP) ⇒ O∈(SBP). O∈l; l║SB; SB⊂(SBP) из всего этого следует, что l⊂(SBP). SP⊂(SBP)
Ну и желательно оговорить почему прямые l и SP не параллельны. l⊥(ABC), BP⊂(ABC) ⇒ l⊥BP. Если l║SP, то SP⊥BP поскольку P∈BP. Получается, что из вершины S проведены две не совпадающие высоты к одной плоскости (ABC), что не возможно. Как итог l не параллельно SP, а раз они лежат в одной плоскости (SBP), то они пересекаются.
Пусть l∩SP=T. T - искомая точка, поскольку T∈SP⊂(SAC)
ответ: l∩(SAC)=T.
Это было доказательство того, что построение верное.
СО - биссектриса и делит угол НСК пополам. .
Центр окружности, вписанной в треугольник АВС, лежит в точке пересечения биссектрис. ВН и СО₁- биссектрисы.
СО₁ делит угол ВСН пополам.
АСК - развернутый угол и равен 180º
Сумма половин углов АСН и ОСН равна половине развернутого угла.
Угол ОСО₁=180°:2=90°⇒
∆ ОСО₁ - прямоугольный с прямым углом С.
АН - высота и медиана равнобедренного треугольника АВС, следовательно, делит основание АС на два равных отрезка:
СН=АН=6.
СН ⊥ АН⇒ является высотой треугольника ОСО₁.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;⇒
СН²=ОН•HO₁
36=8 HO₁
HO₁=36/8=4,5 (ед. длины)