Вся соль решения в том, что треугольник, образованный диагональю (той, которая биссектриса тупого угла), наклонной боковой стороной и большим основанием - равнобедренный. В самом деле, раз диагональ - биссектриса, то она образует с основаниями такой же угол, как и с боковой стороной. :) (угол между ней и большим основанием - это внутренний накрест лежащий угол к углу между ней же и малым основанием).
Поэтому наклонная боковая сторона равна большому основанию, то есть её длина 17.
Если теперь опустить из вершины тупого угла на большое основание перпендикуляр, то получится прямоугольный треугольник с гипотенузой 17 и одним из катетов 17 - 9 = 8. Отсюда второй катет равен 15 (Пифагоров треугольник 8, 15, 17). А это и есть высота трапеции.
Отсюда площадь трапеции равна
15*(17 + 9)/2 = 15*13 = (упражнение для устного счета: = 14^2 - 1 = 195.
Принимаем следующие обозначения:
S1 - площадь осевого сечения цилиндра;
S2 - площадь верхнего основания цилиндра (она также равна нижнего основания цилиндра);
S3 - площадь боковой поверхности цилиндра;
S - площадь всей поверхности цилиндра;
Р - длина окружности верхней грани цилиндра;
R - радиус основания цилиндра;
D - диаметр основания цилиндра.
S=2*S2+S3 общая площадь поверхности равняется сумме двух оснований с площадью боковой поверхности
S1=h*D площадь осевого сечения цилиндра равняется произведению высоты цилиндра на его диаметр основания
D=S1/h=240/20=12 cм
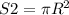
R=D/2=12/2=6 см
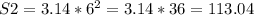 см2
см2
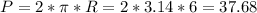 см
см
S3=P*h=37.68*20=753.6 см2
S=2*S2+S3=2*113.04+753.6=979.68 cм2
l=8см
h=√(l²-r²)=√(64-25)=√39
Sосн =πr²=25πсм²
Sбок=πrl=40πсм²
Sпол=Sосн+Sок=25π+40π=65πcм²
V=1/3*Sосн*h=1/3*25π*√39=25π√39/3см³