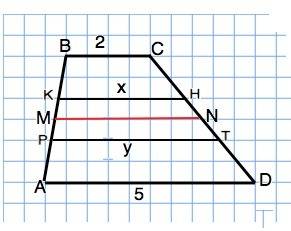
Обозначим трапецию АВСD.
Точки Н и Т делят сторону СD на отрезки
СН=НТ=ТD.
Теорема Фалеса. Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки. ⇒
ВК=КР=РА.
Средняя линия трапеции АВСD - отрезок МN=(ВС+AD):2=(2+5):2=3,5 (м)
СH=HT=TD ⇒
HN=NT, поэтому
MN- средняя линия трапеции РКНТ.
Примем КН=х, РТ=у
Тогда х+у=2•3,5=7, откуда
у=7-х.
КН- средняя линия трапеции РВСТ
КН=(2+(7-х)):2=х
9-х=2х ⇒
х=3 (м) - длина отрезка КН
у=7-3=4 (м) - длина отрезка РТ
Пусть O1 - центр вписанной в треугольник окружности,
r - её радиус
O2 - центр вневписанной окружности, касающейся стороны AC,
R2 - её радиус
O3 - центр вневписанной окружности, касающейся стороны AB,
R3 - eё радиус
p - полупериметр ABC
S = p * r = 8√3
R2 = S / (p - AC) = 8√3
Рассмотрим ΔAO1O2:
пусть O1O2 ∩ AC = K
AC - общая касательная к окружностям с центрами O1 и O2 => точки O1, O2 и K лежат на одной прямой и O1O2 ⊥ AC
AO2 - биссектриса, тк центр вневписанной окружности лежит в точке пересечения биссектрис внешних углов, образованных продолжениями сторон, которых она касается
AO1 - биссектриса, тк центр вписанной окружности лежит в точке пересечения биссектрис
AO1 и AO2 - биссектрисы смежных углов => AO1 ⊥ AO2
Таким образом, AK - высота ΔABC опущенная из прямого угла =>
AK = √(√3*8√3) = 2√6
из ΔAO1K:
по теореме Пифагора
AO1 = 3√3 (o1k - радиус вписанной окружности)
sin∠O1AK = 1 / 3
cos∠O1AK = 2√2 / 3
sin(2∠O1AK) = sin∠BAC = 2sin∠O1AK * cos∠O1AK = 4√2 / 9
Найдем AB из формулы площади:
AB = 2S / (AC * sin∠BAC) = 18√6 / 7
Заметим, что зная сторону AC, нам удалось найти расстояние O1A, значит, зная сторону AB, мы сможем найти искомое O1B
Аналогично:
R3 = 224√3 / (28 - 9√6)
O1O3 ∩ AB = L
BL = √(672 / (28 - 9√6))
по т Пифагора
BO1 = √( (756 - 27√6) / (28 - 9√6) ) = 3√( (84 - 3√6) / (28 - 9√6) )
Полученный результат ~ 27, а периметр = 16
длина биссектрисы никак не может превышать длину периметра, а здесь это только лишь её часть => периметр треугольника с радиусом вписанной окружности √3 не может быть = 16 или наоборот, при фиксированном радиусе, такого периметра быть не может