1. д) через любые три точки проходит плоскость, и притом только одна. (аксиома)
2.д) бесконечно много ( т.е. имеют общую прямую, на которой лежат все общие точки этих плоскостей) или ни одной ( если они параллельны).
3. в) Три данные точки лежат на одной прямой - они принадлежат ей. Через прямую и точку D, не лежащую на этой прямой, можно провести плоскость, притом только одну. ответ:1;
4. в) определяют в любом случае; Через три точки, не лежащие на одной прямой, можно провести плоскость, причём только одну.
5. б) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна;
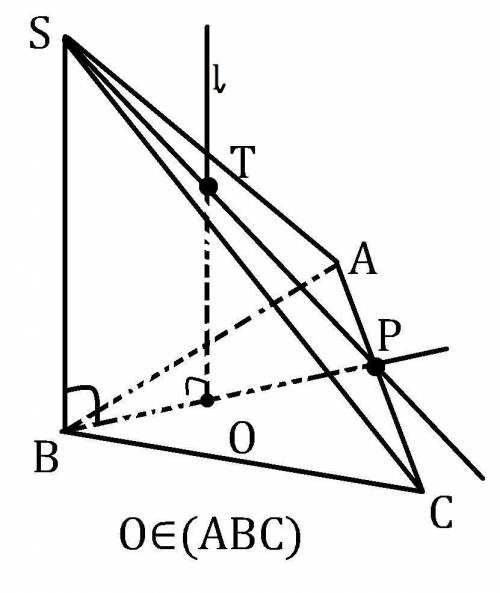
Рисунок к вопросу не был приложен, поэтому возможно пирамида выглядит по другому, но построения нужной точки остаётся правильным.
B,O∈(ABC); BO⊂(ABC); AC⊂(ABC). Пусть BO∩AC=P. *по рисунку O - лежит в треугольнике, поэтому прямые BO и AC не могут быть параллельными, а раз они лежат в одной плоскости, то они пересекаются.
O∈BP⊂(SBP) ⇒ O∈(SBP). O∈l; l║SB; SB⊂(SBP) из всего этого следует, что l⊂(SBP). SP⊂(SBP)
Ну и желательно оговорить почему прямые l и SP не параллельны. l⊥(ABC), BP⊂(ABC) ⇒ l⊥BP. Если l║SP, то SP⊥BP поскольку P∈BP. Получается, что из вершины S проведены две не совпадающие высоты к одной плоскости (ABC), что не возможно. Как итог l не параллельно SP, а раз они лежат в одной плоскости (SBP), то они пересекаются.
Пусть l∩SP=T. T - искомая точка, поскольку T∈SP⊂(SAC)
ответ: l∩(SAC)=T.
Это было доказательство того, что построение верное.
8=a·b·sin30°=a·b·1/2
a·b=16 b=16/a
Периметр равен 2·(a+b)=2·(a+16/a)=2a+32/a
Экстремума функция достигает в точке, где ее производная равна нулю
(2a+32/a)'=2-32/a²=0
2=32/a² a²=16 a=4 (вариант a=-4 не имеет смысла)
Тогда, b=16/a=16/4=4
и минимальный периметр P=2·(a+b)=2·(4+4)=16