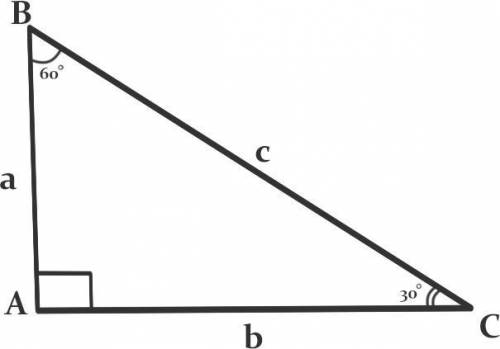
Пусть b - это больший катет (катет, лежащий против угла в 60°), a - меньший катет (катет, лежащий против угла в 30°), с - гипотенуза.
- - -
#1.Теорема Пифагора -
a² + b² = c².
Против угла в 30° лежит катет, равный половине гипотенузы, поэтому -
а = 0,5*с.
Подставим это значение в теорему Пифагора -
(0,5*с)² + b² = с²
0,25*с² + b² = с²
b² = c² - 0,25*с²
b² = 0,75*с²
b = √(0,75*с²)
b = (√0,75)*c.
- - -
#2.b = (b/c)*c
b = sin(∠ABC)*с (по определению синуса острого угла прямоугольного треугольника)
b = sin(60°)*с
b = ((√3)/2)*с
b = (c*√3)/2.
ответ: Верхнее основание 3см
Объяснение: так как углы при основании составляют 45° каждый, то они находятся у нижнего основания и эта это трапеция равнобедренная. Обозначим основание, которое нужно найти -х. Проведём к нижнему основанию высоту с двух вершин верхнего основания. Получился прямоугольный треугольник с углом 45°. Если в прямоугольном треугольнике один угол равен 45° то второй тоже будет 45°, их чего следует,что этот треугольник равнобедренный, и высота равна отрезку при основании. Две высоты, проведённые к нижнему основанию отсекают в нём посередине часть отрезка равную верхнему основанию. Так как трапеция равнобедренная, то отрезки образующиеся на нижнем основании, расположенные по бокам от отрезка равного верхнему основанию, будут равны между собой и их сумма будет составлять 7-х т.е. мы от нижнего основания вычитаем верхнее. Обозначим каждый такой отрезок как (7-х)÷2. Так как мы выяснили, что в прямоугольном треугольнике высота и этот отрезок равны, тогда каждый тоже будет (7-х)÷2. Составляем уравнение:
(7-х)÷2× (7+х)÷2=10
(49-х^)÷4=10
49-х^=40
-х^=40-49
-х^= -9
х^=9
х=3
(7-х)÷2 - это высота; (7+х)÷2- это полусумма двух оснований; 10- это площадь трапеции. Площадь трапеции равна полусумме оснований умноженная на высоту, и на основе этой формулы мы составили уравнение.
Верхнее основание 3.
Мы можем также найти высоту, зная х:
Так как высота равна (7-х)÷2, то
(7-3)÷2=4÷2=2. Высота трапеции 2
Галочки вверху над х^ - читайте как Х в КВАДРАТЕ
1) в первой четверти
sin - монотонно возрастает, cos - монотонно убывает
во второй четверти
синус монотонно убывает, косинус тоже монотонно убывает.
в третьей четверти
синус монотонно убывает, косинус монотонно возрастает
в четвертой четверти
синус монотонно возрастает, косинус монотонно возраствет.
2)
Данное выражение имеет смысл когда подкоренное выражение неотрицательно, то есть:
cos(x)-√3/2≥0
cos(x)≥√3/2
x≥π/6+2πk,k∈Z
x≥-π/6 +2πn, n∈Z
Если нарисовать единичную окружность и отметить точки -π/6, 0, π/6, π/2, то легко заметить, что -π/6 не входит в данный промежуток.
ответ: 0≤x≤π/6
1) в первой четверти
sin - монотонно возрастает, cos - монотонно убывает
во второй четверти
синус монотонно убывает, косинус тоже монотонно убывает.
в третьей четверти
синус монотонно убывает, косинус монотонно возрастает
в четвертой четверти
синус монотонно возрастает, косинус монотонно возраствет.
2)
Данное выражение имеет смысл когда подкоренное выражение неотрицательно, то есть:
cos(x)-√3/2≥0
cos(x)≥√3/2
x≥π/6+2πk,k∈Z
x≥-π/6 +2πn, n∈Z
Если нарисовать единичную окружность и отметить точки -π/6, 0, π/6, π/2, то легко заметить, что -π/6 не входит в данный промежуток.
ответ: 0≤x≤π/6
Катет, лежащий против угла 60 градусов равен:
___________________________________________
Исходя из определения синуса (а он равен отношению противолежащего катета к гипотенузе) можем найти искомый катет.
Тогда MN (искомый катет, лежащий против угла 60 градусов) равен:
MN = sinR * RN
MN = sin60° * RN
____________________________________________
Воспользуемся теоремой Пифагора:
c² = a² + b²
Тогда:
RN² = MN² + RM²
Зная, что катет, лежащий напротив угла 30° равен половине гипотенузы имеем:
RN² = MN² + (0,5RN)²
RN² = MN² + 0,25 * RN²
MN² = 0,75 * RN²
MN = √0,75 * RN²
То есть равен произведению гипотенузы на √3/2.