Рассмотрим трапецию ABCD, образованную стороной шестиугольника, двумя половина сторон шестиугольника и стороной построенного треугольника (то что этот четырехугольник трапеция следует из теоремы Фалеса и условия, что стороны треугольника соеденият середины шестиугольника)
AB=12 см, AD=BC=AB/2=6 см
проведем высоты BK и CN, тогда
BCNK - прямоугольник, треугольники AKB и DNC прямоугольные и равные
BC=KN=12 cм
угол АВС как внутренний угол правильного шестиугольника равен 120 градусов,отсюда
угол АВК равен 120-90=30 градусов, угол ВАК=90-30=60 градусов
Значит AK=AB*cos 60=AB/2=6/2=3 см
(или по свойству треугольника с углами 90,60, 30)
Значит сторона AD=3+12+3=18 см
Аналогично получаем что две другие стороны треугольника равны 18 см, т.е. полученный построением треугольник правильный
Искомая площадь треугольника как площадь правильного треугольника равна
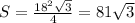 кв.см
кв.см
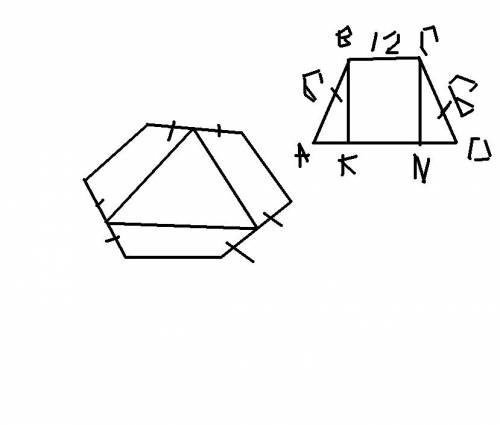
Периметр треугольника, отсекаемого от данного меньшей средней линией, равен полумериметру исходного.
Известны две стороны треугольника.
Третью найдем по теореме Пифагора:
АС= √(АВ²-ВС²)=18 см
Р МВО=(18+24+30):2=36 см
---------------------------------------------
Проекции коротких сторон на длинную делят гипотенузу на два отрезка разной длины.
Для нахождения их воспольземся тем, что Катет - среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу (см.рисунок)
BН=СВ²:АВ=576:30=19,2 см
АН=АС²:АВ=324:30=10,8 см
Проверка:
АН+ВН=19,2+10,8=30 см
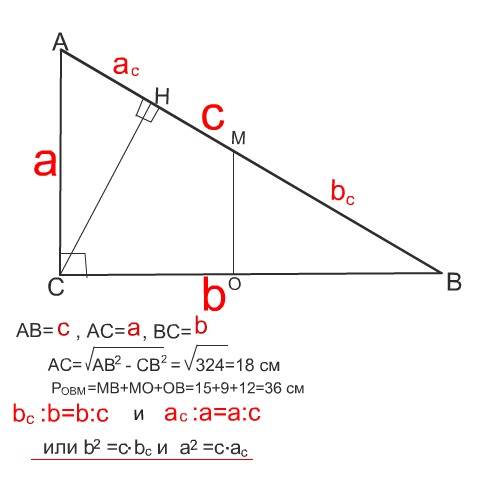
смотри рисунок.
понятно, что отрезки катетов есть отрезки касательных, они равны.
Сделаем все обозначения.
гипотенуза будет 1) х+у=2R
По т. Пифагора
(x+r)²+(y+r)²=(x+y)²
раскрывая, получаем
r(x+y)+r²=xy подставляем сюда 1) и получаем
xy=2Rr+r²
из 1) выделяем у и подставляем, приводим и т.д. и получаем
x²-2Rx+(2Rr+r²)=0
D=4(R²-2Rr-r²)
x=R+/- √(R²-2Rr-r²) но т.к. x≤R то тогда
x=R- √(R²-2Rr-r²)
ну а нижний катет желтого треугольника тогда равен
√(R²-2Rr-r²)
найдем гипотенузу желтого
r²+(√(R²-2Rr-r²) )²=z²
z²=R²-2Rr
z=√(R*(R-2r))
P.S. Здесь я не сделал исследование по поводу допустимых значений радиусов. Просто не захотел, т.к. удлиняет решение.