54 см²
Объяснение:
Позначимо трапецію як АВСД, та висоту із вершини С на основу АД як СК.
Площа прямокутної трапеції складається із площини прямокутника АВСК та площини прямокутного ΔСДК.
Позначимо верхню основу за х, тоді ВС=АК=х і площа АВСК дорівнює СК*ВС=6х; нижня основа трапеції АД=АК+КД=х+КД
В прямокутному ΔСДК відомий катет СК=6 - протилежний куту Д=30°, тому катет КД=СК·ctg∠D=6√3,
в свою чергу гіпотенуза СД=СК÷sin∠D=6·2=12.
Відомо, що, якщо в трапецію можна вписати коло, то сума довжин її осно дорівнює сумі довжин її бічних сторін.
Тоді отримуемо рівняння: ВС+АД=АВ+СД ⇒
х+х+6√3=6+12
х=3·(3-√3)
Тоді площа трапеції:
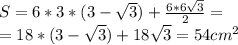
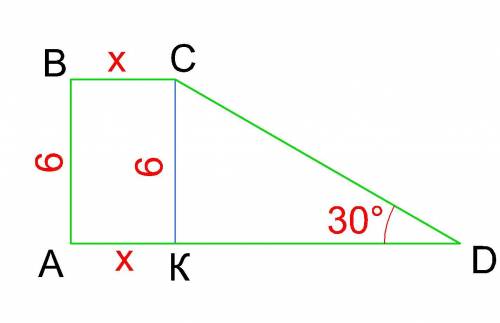
трапеція АВСД, ВС=8, АД=12, ВН=СК-висоти=10, площа АВСД=1/2*(ВС+АД)*ВН=1/2*(8+12)*10=100, площа трикутника АВД=1/2*АД*ВН, площа АСД=1/2*АД*СК(ВН), площа АВД=площа АСД, але площа АВД=площа АОД+площаАОВ, площа АСД=площаАОД+площа СОД, тоді площа АОВ=площаСОД, проводимо перпендикуляр ТР через О, трикутник АОД подібний трикутнику ВОС по двом рівним кутам (кут ВОС=кут АОД як вертикальні, кут ОАД=кутОСВ як внутрішні різносторонні), ОТ -висота в трикутнику ВОС., ОР-висота в трикутнику АОД, в подібних трикутниках сторони пропорційні висотам, ВС/АД=ОТ/ОР, ОТ=х, ТР=ВН, ОР=10-х, 8/12=х/10-х, 12х=80-8х, х=4=ОТ, ОР=10-4=6, площа ВОС=1/2*ВС*ОТ=1/2*8*4=16, площа АОД=1/2*АД*ОР=1/2*12*6=36, площа АОВ=площа СОД=(площаАВСД-площаВОС-площаАОД)/2=(100-16-36)/2=24
С заданными параметрами R и r можно построить два равнобедренных тр-ка, в одном из которых угол при вершине будет меньше шестидесяти градусов, а в другом - больше. Действительно, только в равностороннем треугольнике центры вписанной и описанной окружностей совпадают, а в нашем, равнобедренном треугольнике, они расположены отдельно, и лежат на высоте, проведённой к основанию.
Для обоих треугольников расстояние между центрами вписанной и описанной окружности можно вычислить по формуле Эйлера:
d²=R²-2Rr, где d=О1О2.
d²=25²-2·25·12=25,
d=5 см.
Пусть АС=а, АВ=ВС=b.
Из формулы S=abc/2R имеем при а=b:
S=b²с/2R ⇒ b²=2RS/c.
Также S=ch/2, значит
b²=2Rch/(2c)=2Rh.
Рассмотрим два варианта отдельно.
1) ∠В<60°, тогда h>R+r.
h=ВМ=ВО1+О1О2+МО2=R+d+r=25+5+12=42.
b²=2·25·42=2100,
b=10√21 см.
В тр-ке АВМ АМ=√(АВ²-ВМ²)=√(2100-42²)=√336=4√21.
Периметр АВС: Р=2(АВ+АМ)=2(10√21+4√21)=28√21 см - это ответ.
2) ∠В>60°, тогда h<R+r.
Так как d<r или О1О2<МО2, то центр описанной окружности лежит внутри треугольника АВС.
h=ВМ=ВО1+МО2-О1О2=R+r-d=25+12-5=32 cм.
b²=2·25·32=1600,
b=40 см.
В тр-ке АВМ АМ=√(АВ²-ВМ²)=√(40²-32²)=24 см.
Периметр АВС=2(АВ+АМ)=2(40+24)=128 см - это ответ.