Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
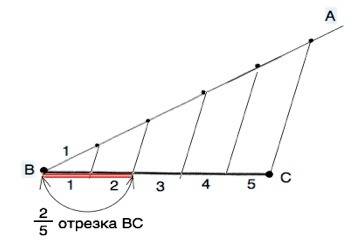
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
<ACD=<ACB по условию.
<CAD=<ACB - накрест лежащие при AD||BC и секущей АС,
=> <CAD=<ACD, ΔADC - равнобедренный. AD=CD
AD=CD=BC=x см
P=AB+BC+CD+AD
84=x+6+x+x
3x=78
x=26
AB=CD=AD=26 см
BM_|_AD, CN_|_AD
MN=BC=6 см
AM=NC=(AD-MN)/2
AM=10 см
ΔAMB: <AMB=90°, AM=10 см, AB=26 см
по теореме Пифагора: AB²=ВМ²+AM²
BM=24 см