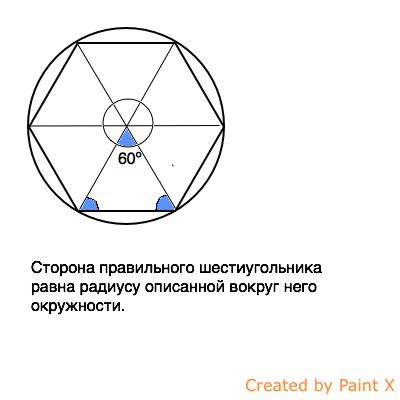
Сторона правильного шестиугольника, вписанного в окружность с радиусом 1, тоже равна 1.
Объяснение:
Так как шестиугольник можно разбить на 6 треугольников, у которых сторонами будут стороны самого шестиугольника и прямые, проведенные от центра шестиугольника к каждому из его углов. Эти маленькие треугольники будут равносторонними. Так как углы при вершине центра шестиугольника будут равны 360°:6=60°. А сам треугольник, считая основанием сторону шестиугольника, будет равнобедренным, так как сторонами будут радиусы описанной окружности. Так как в треугольнике сумма углов 180°, то на эти углы приходится 180°-60°=120°. Так как углы при основании равны, то 120°:2=60° - на каждый из оставшихся углов. Значит каждый из углов равен 60°. Это возможно в равностороннем треугольнике. Значит радиус равен стороне шестиугольника.
дано а=10, h=6
найти b
второй катет будем искать через площадь треугольника.
Площадь треугольника можно найти по формуле через высоту S=1/2 * c * h
С другой стороны, площадь прямоугольного треугольника можно выразить через катеты S=1/2 * a * b
значит 1/2 * c * h = 1/2 * a * b
с * h = a * b
√(a² + b²) * h = a * b возводим в квадрат обе части
(a² + b²) * h² = a² * b²
a² * h² = b² ( a² - h²)
b = √((a² * h²) / (a² - h²) )= a * h / √(a² - h²) = 10*6/√64 = 7,5