Площадь квадрата равна 8 ед²
Объяснение:
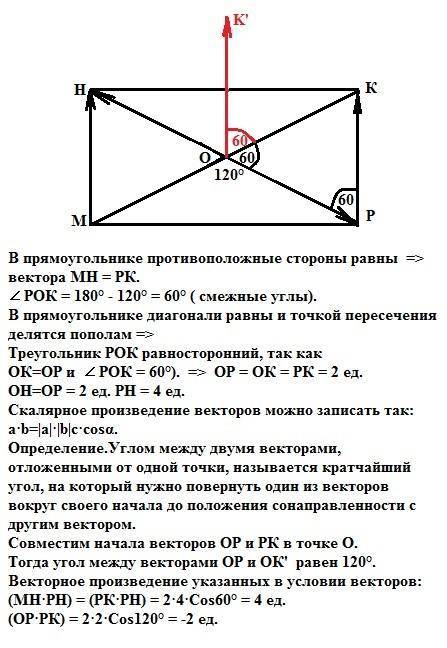
Дано
Окружность
АBCDEF- шестиугольник вписанный
KLMN- квадрат вписанный.
SABCDEF=6√3 ед²
SKLMN=?
Решение
Шестиугольник состоит из 6 равносторонних треугольников.
Найдем площадь одного треугольника.
S∆ABO=SABCDEF/6=6√3/6=√3 eд² площадь одного треугольника.
Из формулы равностороннего треугольника
S=a²√3/4, где а -сторона треугольника.
Найдем сторону треугольника.
а=√(4S/√3)=√(4√3/√3)=2 ед сторона треугольника
а=АО=R=2ед.
КМ диагональ квадрата равна диаметру окружности.
КМ=2*АО=2*2=4 ед. диагональ квадрата.
Из формулы нахождения диагонали квадрата
КМ=КN*√2.
Найдем сторону квадрата.
КN=KM/√2=4/√2=2√2 сторона квадрата.
SKLMN=KN²=(2√2)²=4*2=8 ед² площадь квадрата
(МН·РН) = 4 ед.
(ОР·РК) = -2 ед.
Объяснение:
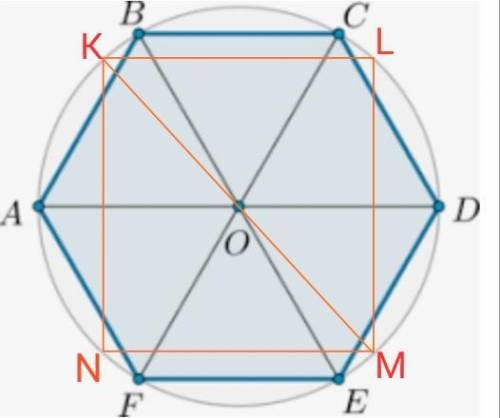
В прямоугольнике противоположные стороны равны =>
вектора МН = РК.
∠ РОК = 180° - 120° = 60° ( смежные углы).
В прямоугольнике диагонали равны и точкой пересечения делятся пополам =>
Треугольник РОК равносторонний, так как
ОК=ОР и ∠ РОК = 60°). => ОР = ОК = РК = 2 ед.
ОН=ОР = 2 ед. РН = 4 ед.
Скалярное произведение векторов можно записать так:
a·b=|a|·|b|c·сosα.
Определение: "Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором".
Совместим начала векторов ОР и РК в точке О. Тогда угол между векторами ОР и ОК' (вектора ОК и ОК' равны) равен 120°.
Векторное произведение указанных в условии векторов:
(МН·РН) = (РК·РН) = 2·4·Cos60° = 4 ед.
(ОР·РК) = 2·2·Cos120° = -2 ед.