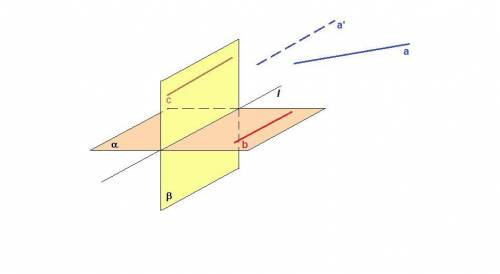
Предположим, что прямая а не пересекает плоскости α и β.
Значит, прямая а параллельна обеим плоскостям.
Тогда в каждой плоскости найдется прямая, параллельная прямой а. Пусть это прямые b и с.
Так как b║a и с║а, то b║c.
Если прямая с параллельна прямой b, лежащей в плоскости α, то с║α.
Плоскость β проходит через прямую с, параллельную плоскости α, и пересекает плоскость α, значит линия пересечения плоскостей параллельна прямой с.
Итак, c║l, c║a, ⇒ l║a. Но прямые l и а скрещивающиеся. Получили противоречие.
Значит, прямая а пересекает хотя бы одну из плоскостей.
Дано:
ABC - равнобедренный треугольник
Угол B=120 градусов
AC=8 см
Найти:
AB -?
Пусть точка D - середина стороны АС
Проведем высоту AD
Рассмотрим треугольник ADB
По свойству медианы треугольника, угол ABD=60 градусов;
Т.к. треугольник ABC равнобедренный, то угол BAD=30 градусов
Из этих условий следует, что треугольник ABD - прямоугольный
AB=AD/sin B
AB=8
Сторона AB треугольника ADB является также стороной треугольника ABC
ответ: AB=8см