Объяснение:
Дано:
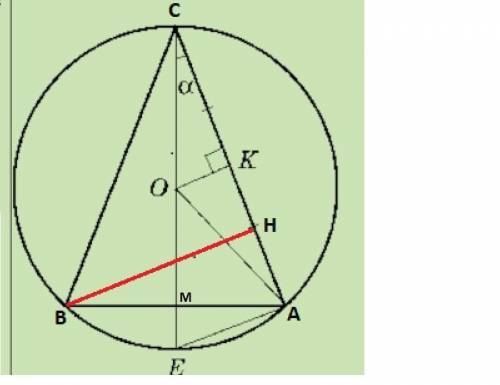
АH=12 см, АВ=13 см, D = 26 = 2r
BC = ?
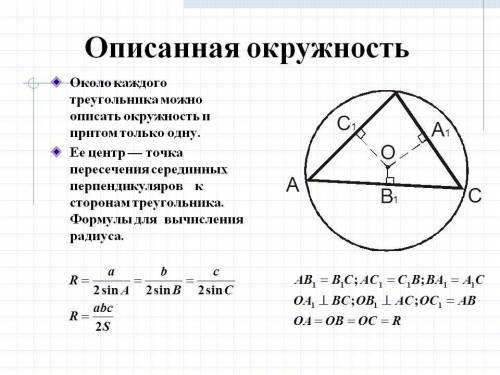
описанная окружность с центром на серединных перпендикуляров .
для вписанного в окружность Δ R= (a*b*c)/ (2S)
АК = КС = 1/2 *АС; АМ = МВ = 1/2 *АВ
из ΔАОМ ; ОМ = √(АО^2 - AM^2) = √(13^2 - (13/2)^2)= √[(13^2* (1- 1/4)]
OM = 6.5√3 то есть АО- гипотенуза, АМ - 1/2*АО , ⇒ ∠АОМ = 30° .
ΔАОВ - равнобедренный АО = ОВ, ∠ОАВ = ∠ОВА = 60 ⇒ ΔАОВ-равносторонний, ⇒ ΔАВС равнобедренный, СМ =медиана, биссектриса, высота. (см рис.2) ⇒ AC = BC
( из ΔBHС ) BH = √(AB^2-BH^2) = √(13^2 - 12^) = √(13+12)(13-12)=√25 = 5
ΔBHA и Δ СКО подобны как Δ с взаимно ⊥ сторонами, а именно
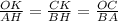
R= (a*b*c)/ (4S) = AC^2* AB / (4SΔавс)
SΔавс 4 1/2*BH*AC
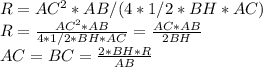
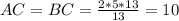

должно быть так
Объяснение:
Так как в основании призмы ромб, а его диагонали, в точке пересечения делятся пополам и пересекаются под прямым углом, то треугольник АОД прямоугольный, АО = АС / 2 = 16 / 2 = 8 см, ОД = 12 / 2 = 6 см.
Тогда, по теореме Пифагора, АД2 = АО2 + ОД2 = 64 + 36 = 100.
АД = 10 см.
Так как призма прямая, то треугольник АДД1 прямоугольный, тогда tg30 = ДД1 / АД.
ДД1 = АД * tg30 = 10 * (1 /√3) = 10 * √3 / 3.
Так как у ромба длины всех сторон равны, то Sбок = 4 * Sаа1д1д = 4 * 10 * 10 * √3 / 3 = 400 * √3 / 3 см2.
ответ: Площадь боковой поверхности равна 400 * √3 / 3 см2.
2)(27-8)+10=29(см)-3 сторона
3)9+27+29=65(см)-периметр