ABCD - прямоугольник, AK - биссектриса, BAK=90/2=45.
В треугольнике с углами 45, 90 стороны относятся как 1:1:√2
AB= AK/√2 =5√2/2
Диагонали прямоугольника равны и точкой пересечения (O) делятся пополам, AO=BO.
△AOB - равнобедренный с углом 60 => равносторонний, ABD=60.
В треугольнике с углами 60, 90 стороны относятся как 1:√3:2
AD= AB*√3 =5√6/2
S(ABCD)= AB*AD =5√2/2 *5√6/2 =25√3/2
проведём диагональ ас, ттогда треугольники асд и авс равнобедренные т к по условию их боковые стороны равны.т.к угол д=39 градусам то угол сад+асд=180-39=141 градус, тогда угол асд=сад=141: 2=70,5 градусам.
рассмотрим треуг. авс:
т.к угол в равен 3 гр,то вас+вса=180-3=177 градусов,по теореме о сумме углов треуг.
т к треуг равнобедренный, то его углы при основании равны,тогда угол вас=вса=177: 2=88,5 градусов
тогда угол а равен сумме углов вас и сад т.е 88.5 градусов+70.5 градусов=159 градусов
ответ: угол а=159 градусов
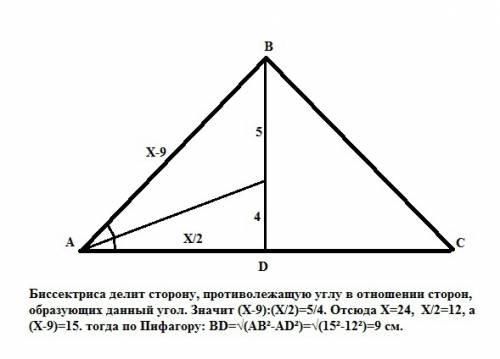
Из треугольника ABK:
∠KAD = ∠BKA(как внутренние накрестлежащие)
∠BAK = ∠KAD (по условию)
Значит, ∠BAK = ∠BKA, тогда треугольник ABK - равнобедренный.
Обозначим катеты как X.
Тогда 2x²=25, x=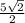 .
.
Проведем AD и BC, обозначим точку пересечения O. Тогда ∠COD = 60°,
CO=DO(по свойству прямоугольника), значит треугольник COD - равносторонний.Значит CD=CO=DO=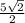 .
.
∠BOC = 180-60=120°, тогда из треугольника BOC по теореме косинусов найдем BC.
BC=√25/2+25/2+25/2=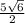 .
.
AB=CD=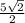 .
.
AD=BC=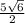 .
.
S=AD*BC=5√3.