ответ: Построение точки пересечения см. на фото.
Объяснение:
Задание относится к "Начертательной геометрии".
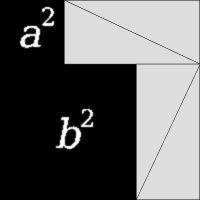
Постройте профильные проекции прямой и треугольника.
Точка 1¹- проекция точки пересечения прямой и плоскости на виде спереди. Найдите проекцию 1¹¹ на виде слева.
Для того, чтобы определить видимость на виде слева, выберем совпадающие точки 2¹¹ и 3¹¹. Получив точки 2¹ и 3¹, видим,что треугольник к наблюдателю ближе, чем прямая. Видимость на виде слева определена.
Найдём проекцию 1 на виде сверху. На виде сверху возьмём совпадающие точки 4 и 5. Найдём их проекции на виде слева: 4¹¹ и 5¹¹. Видя, что 4¹¹, принадлежащая прямой, находится выше, чем 5¹¹ на а¹¹b¹¹, получаем, что на виде сверху в этом месте видна прямая.
Надеюсь, что смогла вам
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора, что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия[⇨]), метод площадей[⇨], существуют также различные экзотические доказательства (например, с дифференциальных уравнений).
Через подобные треугольники
Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры.[10] В нём для треугольника ABC с прямым углом при вершине C со сторонамиa,b,c, противолежащими вершинам A,B,C соответственно, проводится высота при этом согласно признаку подобия по равенству двух углов) возникают соотношения подобия: и , из чего непосредственно следуют соотношения.
При перемножении крайних членов пропорций выводятся равенства:
покомпонентное сложение которых даёт требуемый результат.
(хз надеюсь правильно)