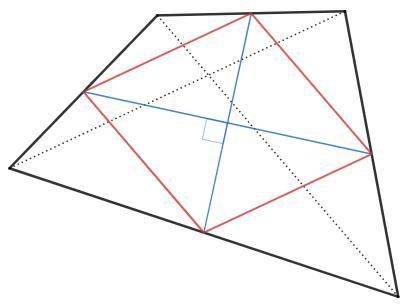
Соединим середины сторон четырехугольника.
Полученные отрезки параллельны диагоналям и равны их половинам, так как являются средними линиями в соответствующих треугольниках.
Отрезки образуют параллелограмм Вариньона.
Площадь четырехугольника Sч =1/2 d₁d₂ sinф
Угол ф между диагоналями четырехугольника равен углу между сторонами пар-ма Вариньона (т.к. они параллельны).
Площадь пар-ма Вариньона Sв =d₁/2 *d₂/2 *sinф =1/2 Sч
Итак, площадь пар-ма Вариньона равна половине площади четырехугольника.
В данном четырехугольнике диагонали равны, следовательно стороны пар-ма Вариньона равны и он является ромбом.
Диагонали ромба перпендикулярны, sin90=1.
Sч =2 Sв =2 *1/2 *14*8 =112
Объяснение:
Параллельность прямых - признаки и условия параллельности.
Признаком параллельности прямых является достаточное условие параллельности прямых, то есть, такое условие, выполнение которого гарантирует параллельность прямых. Иными словами, выполнение этого условия достаточно для того, чтобы констатировать факт параллельности прямых.
Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180 градусам.
Если две прямые на плоскости параллельны третьей прямой, то они параллельны. Доказательство этого признака следует из аксиомы параллельных прямых.
Если две прямые в пространстве параллельны третьей прямой, то они параллельны. Доказательство этого признака рассматривается на уроках геометрии в 10 классе.
Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны
конца вектора и его начала, т е если с(х;y) , то 3=-5-х, х=-5-3=-8,
-2=6-y, y=6+2=8, c(x;y)=c(-8;8)