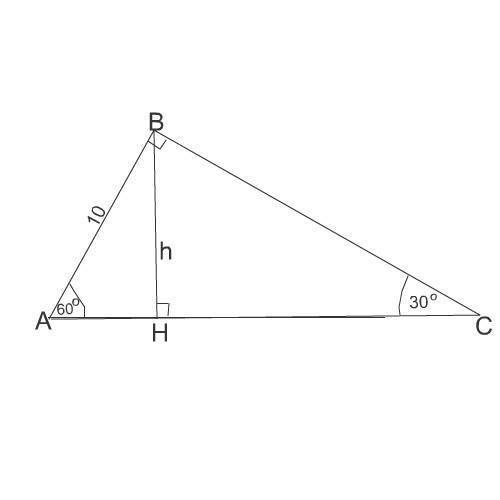
Задачу можно решить по-разному Обозначим вершины треугольника А, В, С, а точку пересечения высоты с гипотенузой - Н.
Найдем гипотенузу.
Так как катет АВ, равный 10 см, противолежит углу 30 градусов, он равен половине гипотенузы, а гипотенуза, соответственно, в два раза больше катета.
Гипотенуза равна 20 см
Катет ВС найдем по теореме Пифагора. Он равен 10√3
Пусть отрезок АН будет х, тогда НС - 20-х
Выразим h² из прямоугольных треугольников АВН и ВСН, образованных катетами, высотой и частью гипотенузы.
h²=АВ²-АН²= 10²-х²
h²=ВС²-НС²=(10√3)²-(20-х)²
Приравняем выражения, найденные для высоты.
10²-х²=(10√3)²-(20-х)²
100-х²=300-400+40х-х²
40х=200
х=5
Подставим значение х в уравнение высоты:
h²=АВ²-х гораздо короче, если мы помним значение синусов некоторых углов.
Рассмотрим треугольник АВС.
Высота, проведенная к гипотенузе, - катет прямоугольного треугольника АВН.
ВН:АВ=sin(60º)
sin(60º)=(√3):2
ВН=АВ*(√3):2=10*(√3):2=5√3
h=5√3
Большее основание равно 32 см.
Объяснение:
Рассматриваем трапецию ABCD - прямоугольная (чтобы было понятней: AB - меньшее основание, DC - большее основание, угол С=45°). Проведём высоту BK к большему основанию из вершины угла B. Получили прямоугольник ADBK. По свойству противоположных сторон BK=AD=16см, AB=DK=16см. Теперь рас-м треугольник BCK - прямоугольный. Т. к. угол C=45°, то найдём угол КВС: (сумма углов Δ - 180°) 180°-(90°+45°)= 45°. Следовательно, Δ BCK -равнобедренный, ВК=СК=16см. DC = DK+KC=16+16=32СМ.
Sокр=pi*R²=pi*a²/2=pi*(64*3)/2=pi*32*3=96*pi ≈ 301,44