1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
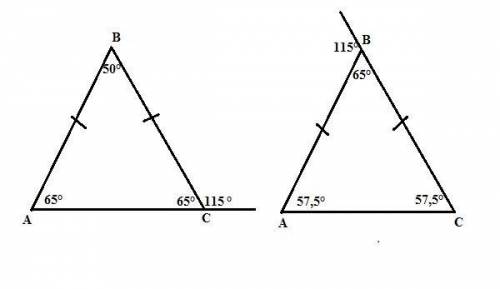
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
Высота правильной четырёхугольной пирамиды равна 12 см, а сторона основания равна 24 см. Вычисли двугранный угол при основании.
——————————————————
Основание правильной четырехугольной пирамиды – квадрат.
Все боковые грани правильной пирамиды образуют с плоскостью основания равные углы, а высота проходит через центр основания, который является центром вписанной и описанной около основания окружностей.
Двугранный угол здесь образован радиусом вписанной окружности и апофемой, как отрезками. перпендикулярными ребру основания в одной точке (по т. о трех перпендикулярах).
Радиус вписанной в квадрат окружности равен половине его стороны.
r=24:2=12 (см)
Соединив основание апофемы с центром основания ( основанием высоты пирамиды), получим прямоугольный треугольник.
При этом катеты- высота пирамиды и половина стороны основания - равны 12 см.
Следовательно, треугольник - равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45º.⇒ Искомый угол равен 45º.
Пусть сторона а=х, значит с=2х, а d=2×2x
x+x+2x+4x=24
8x=24
x=24÷8
x=3
ответ: а=b=3 см, с=6 см, d=12 см