Следом называют прямую пересечения плоскости сечения и плоскости какой-либо грани многогранника.
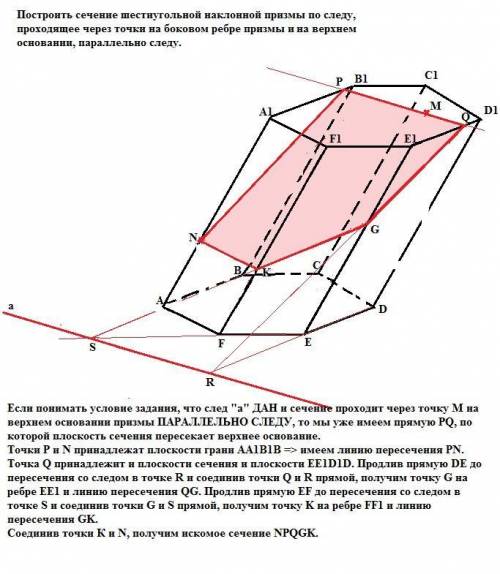
Если понимать условие задания, что след "а" ДАН и сечение проходит через точку М на верхнем основании призмы ПАРАЛЛЕЛЬНО СЛЕДУ, то мы уже имеем прямую PQ, по которой плоскость сечения пересекает верхнее основание.
Точки Р и N принадлежат плоскости грани АА1В1В => имеем линию пересечения PN.
Точка Q принадлежит и плоскости сечения и плоскости EE1D1D. Продлив прямую DE до пересечения со следом в точке R и соединив точки Q и R прямой, получим точку G на ребре ЕЕ1 и линию пересечения QG. Продлив прямую EF до пересечения со следом в точке S и соединив точки G и S прямой, получим точку K на ребре FF1 и линию пересечения GK.
Соединив точки К и N, получим искомое сечение NPQGK.
Решение задачи во многом зависит от выбора точек.
Поэтому либо нужен рисунок, на котором расположены точки, либо надо рассмотреть разные случаи.
Итак,
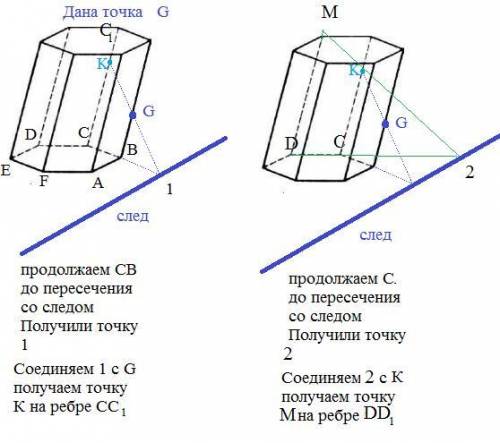
Если точка G на ребре ВВ₁ ближе к нижнему основанию cм. рис., то легко построить точку К на ребре СС₁.
Так как проекцией точки G является точка В, а проекцией искомой точки К - точка С, то
соедив проекции, т.е В с С и продолжив до пересечения со следом, получим точку 1.
Соединяем точку 1 с точкой G получаем точку К.
И так далее.
Главное:
прямые, содержащие точки секущей плоскости и прямые содержащие их проекции пересекаются на прямой, называемой СЛЕДОМ.
Через точку, лежащую на верхнем основании, проводим прямую, параллельную следу.
Получим 2 точки на сторонах верхнего основания.
Эта точка должна быть так выбрана, чтобы не было противоречия с положением точки К
См. рис. точка N на верхнем основании.
Проводим через точку N прямую, параллельную следу.
Эта прямая пересекает верхнее основание в точках P и Т.
Проекция точки Р лежит на ЕА.
Продолжаем ЕА до пересечения со следом, получаем точку на следе. Соединяем эту точку с точкой Р и получаем точку на ребре АА₁
Аналогчно получим точку на ребре СС₁
Сечение
PTQR- параллельно следу, проходит через точку N на верхнем основании, но не проходит через точку G, на ребре ВВ₁, выбранную в первом случае.
Сумма всех углов параллелограмма равна 360°.
АВСД - параллелограмм, ∠А=∠С, ∠В=∠Д
∠А+∠В+∠С+∠Д=360°
Допустим, что ∠В=∠Д=107°
Значит
∠А+∠В+∠С+∠Д=360° и ∠В=∠Д, значит
∠А+107°+∠С+107°=360°
∠А+∠С=360°-214°
2∠А=146°
∠А=∠С=146°/2
∠А=∠С=73°.
Периметр параллелограмма = сумме всех его сторон.
Допустим, что ВК - биссектриса, а она делит угол пополам, значит ∠АВК=∠СВК=0,5*∠АВС=0,5*107°=53,5°.
Рассмотрим треугольник АВК, в нем
∠А=73°
∠В=53,5°.
АК=8 см
Сумма углов любого треугольника равна 180°, то есть
∠А+∠В+∠К=180°
73°+53,5°+∠К=180°
∠К=180°-126,5°
∠К=53,5°
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, т.е. в треугольнике АВК
АК/sin∠В=АВ/sin∠К, отсюда
АВ=АК*sin∠К/sin∠В.
Поскольку ∠К=∠В=53,5°, то и sin∠К=sin∠В, выходит, что
sin∠К/sin∠В=1, а это значит
АВ=АК*sin∠К/sin∠В
АВ=АК=8 см.
АД=АК+ДК=8+12 см=20 см
Поскольку у любого параллелограмма противоположные стороны равны, значит
АВ=СД=8 см
ВС=АД=20 см.
Периметр параллелограмма = сумме всех его сторон, то есть
Р=АВ+ВС+СД+АД=8+20+8+20=56 см.
ответ: ∠А=∠С=73°;
∠В=∠Д=107°;
Периметр параллелограмма = 56 см.