В равнобедренном треугольнике углы при основании равны. ∠ВАС=∠ВСА
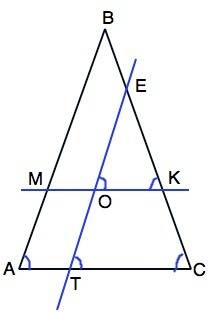
Обозначим данный треугольник АВС; О - точку пересечения прямых ЕТ||АВ и МК||АС.
АС секущая при ВА║ЕТ ⇒
∠ЕТС=∠ВАС как соответственные.
ЕТ секущая при МК║АС⇒
∠ЕОК=∠ЕТС как соответственные, следовательно, ∠ЕОК=∠ВАС.
ВС секущая при МК||АС⇒
∠ЕКО=∠ВСА, как соответственные. .
Следовательно, ∠ЕКО=∠ЕОК. что является признаком равнобедренного треугольника. ⇒
Треугольник ЕОК равнобедренный с углами при основании, которые равны углам при основании АС треугольника АВС.
№1 трапеция АВСД, СД=25, ОД=15, ОВ=9, треугольник АОВ подобен треугольнику ДОС по двум равным углам (уголАОВ=уголДОС как вертикальные, уголДСО=уголВАО как внутренние разносторонние), АВ/СД=ОВ/ОД, АВ/25=9/15, АВ=25*9/15=15, ДС/АВ=ОС/ОА, 25/15=ОС/ОА, 5/3=ОС/ОА, площади подобных треугольников относятся как квадраты подобных сторон, площадь АОВ/площадь ДОС=АВ в квадрате/СД в квадрате=225/625=9/25
№2 треугольник АВС подобен трецугольнику КМН по третьему признаку (три стороны одного треугольника пропорцианальны трем сторонаим другого), АВ/КМ=8/10=4/5, ВС/МН=12/15=4/5, АС/КН=16/20=4/5, пропорции равны, вподобных треугольниках против подобных сторон лежат равные углы, уголА=уголК=80, уголВ=уголМ=60, уголС=уголН=(180-80-60)=40
№3 трапеция АВСД, ВС=4, АД=12, площадь АОД=45, треугольник ВОС подобен треугольнику АОД по двум равным углам (уголВОС=уголАОД как вертикальные, уголОАД=уголВСО как внутренние разносторонние), площади относятся как квадраты сторон, ВС/АД=4/12=1/3, площадь ВОС/площадь АОД=(ВС/АД) в квадрате, площадь ВОС/45=1/9, площадь ВОС=45*1/9=5
2х+7=33
2х=26
х=13
ав=13 вс=20