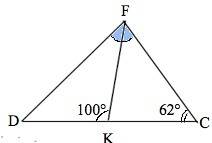
Угол FKD для ∆FKC- внешний и равен сумме двух несмежных с ним углов.
62°+CFK=100°
CFK=100°-62°=38°
FK- биссектриса, след. угол ВАС=2₽38°=76°
* * *
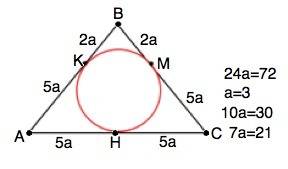
Отрезки касательных, проведенных из одной точки, равны.
АК=АН,ВК=ВМ, СК=СМ.
Примем коэффицинент отношения отрезков сторон равным а. Тогда АН=АК=5а, СН=СМ=5а,
ВК=ВМ=2а
Периметр ∆ АВС=24а
24а=72а
а=3
АВ=ВС=3•(2+5)=21 см,
АС=3•(5+5)=30см
* * *
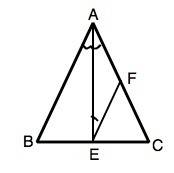
Треугольник АВС - равнобедренный.
АF=FE. ∆ АЕF – равнобедренный, угол ЕАD=AFE.
АЕ - высота равнобедренного треугольника, она же – его медиана и биссектриса.
∠ВАЕ=∠АЕF. эти углы - накрестлежащие. Если при пересечении двух прямых накрестлежащие углы равны. эти прямые - параллельны.
EF || АВ, ч.т.д.
12. Нет ни одного правильного варианта ответа.
12.1 Правильная формулировка: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
12.2 Правильная формулировка: Тупоугольным называют треугольник, у которого один из углов тупой, то есть его градусная мера больше (а не равна) 90 градусов.
12.3 Доказательство: схематически если вы нарисуете ромб не совсем стандартной формы, вы сразу поймете что диагонали не будут перпендикулярны. Одни могут быть длиннее других.
13. Правильные варианты ответа: 1, 3
13.2 Правильная формулировка: Не в любой четырёхугольный треугольник можно вписать окружность. Вписать окружность можно только в правильный четырехугольник. Правильный многоугольник - это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны.
14. Правильные варианты ответа: 2
14.1 Правильная формулировка: В добавок в этому надо еще разделить на два.
14.3 Правильная формулировка: Можно описать в параллелограмм окружность только если сумма противоположных углов равно 180 градусам.
15. Правильные варианты ответа: 1, 2, 3
16. Правильные варианты ответа: 1, 3
16.2 Правильная формулировка: Это подходит тогда, когда прямоугольник является квадратом.
P.s: Рад был
P.s.s: Спустя два года))
Объяснение:
Аксиома: через две любые точки плоскости можно провести прямую и притом только одну.
Из аксиомы следует, что если две прямые имеют две (или более) общих точек, то они совпадают. А в задаче речь идет о двух различных прямых.
Если две прямые на плоскости имеют одну общую точку, то они пересекаются.
Если две прямые на плоскости не имеют общих точек, то они параллельны.
Итак, две различные прямые на плоскости могут либо пересекаться, либо быть параллельными.