Ну, я надеюсь, дано ты запишешь сам. Вот решение, как сделаешь рисунок, все будет понятно: т.к. угол DAC=30 градусам, значит катет лежащий на против него равен половине гипотенузы (а она АС равна 12), а значит DC равен 6. Т. к. ABCD прямоугольник, значит и противоположная сторона АВ равна тоже 6. АС диагональ и она делится в точке пересечения по палам и следовательно АО = 6. В треугольнике АОВ все углы 60, т.к. угол DAO = 30 и следовательно угол ОАВ равен 90-30=60, и значит все углы тоже равны 60. И значит периметр треугольника равен 6+6=6= 18. Вот и все.
Найдите периметр треугольника с площадью 10√3 см² и углом 60°, если стороны, прилежащие к данному углу, относятся как 5:8.
Объяснение:
Пусть в ΔАВС , ∠В=60° , АВ:ВС=5:8.
Если одна часть х см , то АВ=5х, ВС=8х.
S( треуг.) = 1/2*АВ*ВС*sinВ или 10√3=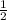 
*5х*8х*
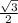, х²=1 , х=1 ⇒
АВ=5 см , ВС=8 см .
По т. косинусов АС²=АВ²+ВС²-2*АВ*ВС*cosВ,
АС²=25+64-2*5*8*cos60, АС²=89-2*5*8*1/2, АС=7 см
Р=5+8+7=20 ( см)
====================
S( треуг.) = 1/2*а*в* sinα
Т. косинусов "Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними"
На рисунке в файле картинка этого сечения - равнобедренный треугольник. У него b=10, a=16. Свойство высоты такого треугольника (она же высота конуса) - делить основание (16) пополам на отрезки 8 и 8 ед. Тогда получим два прямоугольных треугольника с гипотенузами b=10 и катетом a/2=8. По теореме Пифагора находим h=корень из b*b-(a/2*a/2)= корень из(100-64)=корень из 36=6
ответ: H=6