Геометрия: Луч вd делит прямой угол abc на 2 угла которые относятся 3: 6

Луч вd делит прямой угол abc на 2 угла которые относятся 3: 6

👇

Ответ:

КириллSOS

06.12.2020

Прямой угол = 90 градусов
пусть одна часть будет х
значит, 3х+6х=90
9х=90
х=10
значит, угол ABD = 3*10 =30
угол DBC = 6*10=60

4,4(44 оценок)

Открыть все ответы

Ответ:

notix55

06.12.2020

ответ:

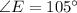
$\angle E=105^{\circ}$

Объяснение:

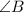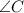Проведём биссектрисы $\angle B$ и $\angle C$ . Пусть они пересекаются в точке .

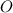Также проведём отрезки 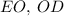$EO, \: OD$ и .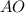

========================================

Рассмотрим 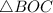$\triangle BOC$ :

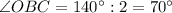$\angle OBC = 140^{\circ}:2=70^{\circ}$ , т.к. 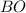- биссектриса.

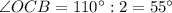$\angle OCB=110^{\circ}:2=55^{\circ}$ , т.к. 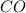- биссектриса.

Сумма внутренних углов треугольника равна 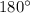$180^{\circ}$ .

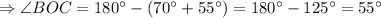
$\Rightarrow \angle BOC=180^{\circ}-(70^{\circ}+55^{\circ})=180^{\circ}-125^{\circ}=55^{\circ}$

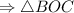$\Rightarrow \triangle BOC$ - равнобедренный.

========================================

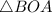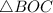Рассмотрим $\triangle BOA$ и $\triangle BOC$ :

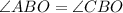$\angle ABO=\angle CBO$ , т.к. 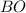- биссектриса;

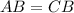AB=CB (по условию); 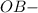OB - общая сторона.

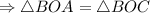$\Rightarrow \triangle BOA=\triangle BOC$ (по I признаку равенства треугольников).

========================================

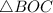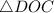Рассмотрим $\triangle BOC$ и $\triangle DOC$ :

$\angle BCO=\angle DCO$ , т.к. 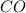- биссектриса;

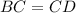BC=CD (по условию), 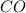- общая сторона.

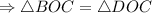$\Rightarrow \triangle BOC=\triangle DOC$ (по I признаку равенства треугольников).

========================================

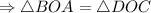$\Rightarrow \triangle BOA=\triangle DOC$ , т.е. мы имеем три равных равнобедренных тр-ка:

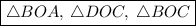
$\boxed{\triangle BOA, \: \triangle DOC,\: \triangle BOC}$

========================================

Рассмотрим 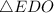$\triangle EDO$ :

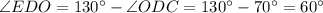$\angle EDO=130^{\circ}-\angle ODC=130^{\circ}-70^{\circ}=60^{\circ}$ .

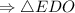$\Rightarrow \triangle EDO$ - равносторонний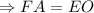 $\Rightarrow FA=EO$

========================================

Рассмотрим геометрическую фигуру 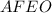AFEO :

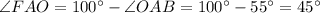$\angle FAO=100^{\circ}-\angle OAB=100^{\circ}-55^{\circ}=45^{\circ}$ .

$\angle AOE=360^{\circ}-(55^{\circ}+55^{\circ}+55^{\circ}+60^{\circ})=135^{\circ}$ (т.к. в полном угле всего 360°)

При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 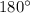$180^{\circ}$ .

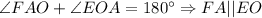
$\angle FAO+\angle EOA=180^{\circ} \Rightarrow FA|| EO$

Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.

У параллелограмма противоположные углы равны.

$\Rightarrow \angle FAO=\angle FEO=45^{\circ}$ .

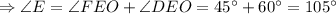
$\Rightarrow \angle E=\angle FEO+\angle DEO=45^{\circ}+60^{\circ}=105^{\circ}$

========================================

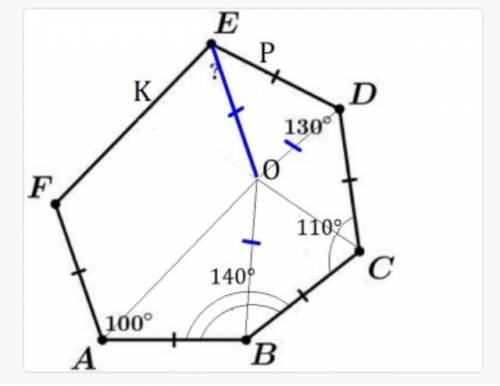
В шестиугольнике ABCDEF выполнены равенства FA=AB=BC=CD=DE, ∠A=100∘, ∠B=140∘, ∠C=110∘, ∠D=130∘. Найд

4,7(41 оценок)

Ответ:

Лиза22092004

06.12.2020

Пусть LC=2x, тогда BL=7x

КТ=BL=7x(по свойствам параллелограмма)
Теперь рассмотрим треугольники АВС и АКТ
угА=уг.А(общий)
угАКТ=угАВС(т. к. это соответственные углы при параллельных КТ и АС, параллельны они потому что КТ||BL по свойствам параллелограмма, а прямая АС содержи BL)
Следовательнор АКТ подобен АВС, отсюда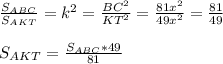
$\frac{S_{ABC}}{S_{AKT}}=k^2=\frac{BC^2}{KT^2}=\frac{81x^2}{49x^2}=\frac{81}{49}\\\\S_{AKT}=\frac{S_{ABC}*49}{81}$

Теперь рассмотрим треугольники АВС и LTC
угC=уг.C(общий)
угCLT=угABC(т. к. это соответственные углы при параллельных LТ и АB, параллельны они потому что LТ||BK по свойствам параллелограмма, а прямая АB содержи BK)
Следовательнор LCТ подобен АВС, отсюда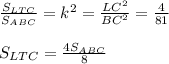
$\frac{S_{LTC}}{S_{ABC}}=k^2=\frac{LC^2}{BC^2}=\frac{4}{81}\\\\S_{LTC}=\frac{4S_{ABC}}{8}$
Но нам известно что Sabc=Sakt+Sltc+Skblt Отсюда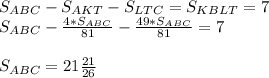
$S_{ABC}-S_{AKT}-S_{LTC}=S_{KBLT}=7\\S_{ABC}-\frac{4*S_{ABC}}{81}-\frac{49*S_{ABC}}{81}=7\\\\S_{ABC}=21\frac{21}{26}$