Объяснение:
Для доказательства потребуются признаки равенства треугольников.
Признаки параллелограмма.
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
1. Противоположные стороны попарно равны ( AB = CD, AD = BC ).
2. Противоположные углы попарно равны ( A = C, B = D )
3. Две противоположные стороны равны и параллельны ( AB = CD, AB || CD )
4. Диагонали делятся в точке их пересечения пополам ( AO = OC, BO = OD)
Признак: "Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм".
Стороны АВ=СD (дано). Углы ВАС и АСD равны (дано). Это накрест лежащие углы при прямых АВ и CD и секущей АС. Следовательно, эти прямые параллельны (признак). АВСD - параллелограмм по приведенному выше признаку. Что и требовалось доказать.
2. Треугольники ADB и DCB равны по двум углам (<1=<4 и <2=<3 - дано) и стороне между ними - DB - общая. В равных треугольниках против равных углов лежат равные стороны.
AD=CB, DC=AB. ABCD - параллелограмм по признаку: "Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
ЧТД.
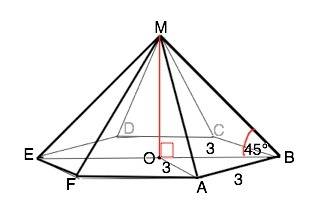
Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.
Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольников со стороной 3 см.
Обозначим пирамиду ABCDEF, центр - О.
Высота МО и половина ВО диагонали ВЕ образуют прямоугольный треугольник МОВ, острый угол МВО=45°. ⇒ Это равнобедренный треугольник, и МО=ВО=3 см.
Объём пирамиды равен 1/3 произведения высоты на площадь основания.
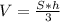
Площадь правильного шестиугольника – сумма площадей 6 правильных треугольников, площадь которых найдем по формуле:
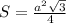
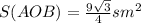
Площадь основания
6•9√3/4 sm²
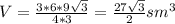
Мы знаем BE(2 корень из 3) и AD=BC=3 =>
По теореме Пифагора:
ЕС в квадрате=BE( тоже в квадрате)-BC( тоже в квадрате)
ЕС в квадрате=12-9=3
ЕС= корень из 3