Даны векторы m(2; p) и n(9; -3). при каком значении p векторы m и n: 1) коллинеарны 2)перпендикулярны?

👇

Увидеть ответ

Ответ:

duyquhuseynli11

20.05.2022

1) -4 колинеарние

4,4(25 оценок)

Открыть все ответы

Ответ:

zhzdd

20.05.2022

Объяснение:

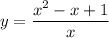
$\displaystyle y=\frac{x^2-x+1}{x}$

1. ОДЗ: х≠0;

или х ∈ (-∞; 0) ∪ (0; +∞)

2. Четность, нечетность.

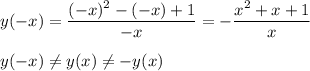
$\displaystyle y(-x)=\frac{(-x)^2-(-x)+1}{-x}=-\frac{x^2+x+1}{x}y(-x)\neq y(x)\neq -y(x)$

⇒ функция не является четной или нечетной, то есть - общего вида.

3. Пересечение с осями.

1) х ≠ 0 ⇒ ось 0у не пересекает.

2) у = 0 ⇒

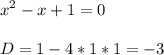
$\displaystyle x^2-x+1=0D=1-4*1*1=-3$

⇒ корней нет, то есть ось 0х не пересекает.

4. Асимптоты.

1) Вертикальная.

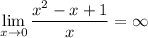
$\displaystyle \lim_{x \to 0} \frac{x^2-x+1}{x}=\infty$

⇒ x=0 - вертикальная асимптота.

2) Наклонная: у = kx + b

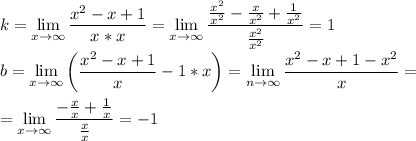
$\displaystyle k= \lim_{x \to \infty} \frac{x^2-x+1}{x*x}= \lim_{x \to \infty} \frac{\frac{x^2}{x^2}-\frac{x}{x^2}+\frac{1}{x^2} }{\frac{x^2}{x^2} } =1b= \lim_{x \to \infty} \left(\frac{x^2-x+1}{x}-1*x\right)= \lim_{n \to \infty} \frac{x^2-x+1-x^2}{x}== \lim_{x \to \infty} \frac{-\frac{x}{x}+\frac{1}{x} }{\frac{x}{x} }=-1$

⇒ y = x - 1 - наклонная асимптота.

5. Возрастание, убывание, экстремумы.

Найдем производную, приравняем к 0, найдем корни и отметим их на числовой оси. Определим знаки производной на промежутках. Если "+" - возрастает, если "-" - убывает.

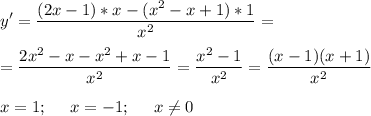
$\displaystyle y'=\frac{(2x-1)*x-(x^2-x+1)*1}{x^2} ==\frac{2x^2-x-x^2+x-1}{x^2} =\frac{x^2-1}{x^2}=\frac{(x-1)(x+1)}{x^2}x=1;\;\;\;\;\;x=-1;\;\;\;\;\;x\neq 0$

$\displaystyle [-1](0)[1]$

Возрастает при х ∈ (-∞; -1] ∪ [1; +∞)

Убывает при х ∈ [-1; 0) ∪ (0; 1]

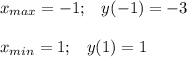
$\displaystyle x_{max}=-1; \;\;\;y(-1)=-3x_{min}=1;\;\;\;y(1)=1$

6. Выпуклость, вогнутость.

Найдем производную второго порядка.

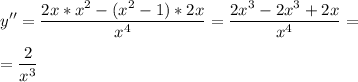
$\displaystyle y''=\frac{2x*x^2-(x^2-1)*2x}{x^4}=\frac{2x^3-2x^3+2x}{x^4}==\frac{2}{x^3}$

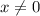
$\displaystyle x\neq 0$

Найдем знак второй производной на промежутках. Если "+" - вогнута, если "-" - выпукла.

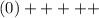
$\displaystyle (0)$

Выпуклая при х ∈ (-∞; 0)

Вогнутая при х ∈ (0; +∞)

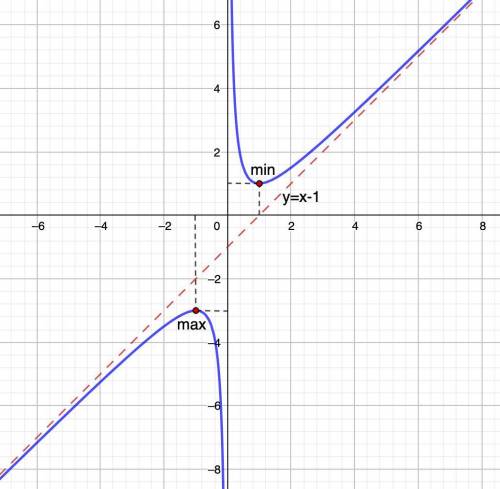
Строим график.

очень Нужно сделать исследование функции и построить график

4,4(58 оценок)

Ответ:

natik2005

20.05.2022

Призма

Призмой называется многогранник, две грани которого n-угольники, а остальные n граней — параллелограммы.Боковые ребра призмы равны и параллельны.

Перпендикуляр, проведенный из какой-либо точки одного основания к плоскости другого основания, называется высотой призмы. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.Поверхность призмы состоит из оснований и боковой поверхности призмы. Боковая поверхность призмы состоит из параллелограммов.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой. В противном случае призма называется наклонной.

У прямой призмы боковые грани – прямоугольники.

Высота прямой призмы равна ее боковому ребру.

Прямая призма называется правильной, если она прямая, и ее основания — правильные многоугольники

Площадь поверхности и объём призмы

Пусть H — высота призмы, — боковое ребро призмы, — периметр основания призмы, площадь основания призмы, — площадь боковой поверхности призмы, — площадь полной поверхности призмы, - объем призмы, — периметр перпендикулярного сечения призмы, — площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований, площадь боковой поверхности и объем даются формулами:

Параллелепипед

Параллелепипедом называется призма, основанием которой является параллелограмм.

Параллелограммы, из которых составлен параллелепипед, называются его гранями, их

4,6(80 оценок)

Это интересно:

Образование

06.01.2021

Клюква стоит 250 рублей за кг, а малина 200....

Образование

16.03.2023

Решить систему уравнений x2 + y2 + xy = 3...