russian.
тригонометрические функции острого угла в прямоугольном треугольнике. sin, cos, tg, ctg
итак, у каждого прямоугольного треугольника есть два острых угла. для каждого из них можно найти синус, косинус, тангенс и котангенс. здесь главное не перепутать, что к чему относится.
синус острого угла пр. треугольника - это отношение (деление) противолежащего этому углу катета к гипотенузе.
косинус острого угла пр. треугольника - это отношение (деление) прилегающего к этому углу катета к гипотенузе.
тангенс острого угла пр. треугольника - это отношение противолежащего этому углу катета к прилегающему катету.
котангенс - это наоборот, отношение прилегающего к этому углу катета к противолежащему.
во вложении есть рисунок, там все показано. легче это понять словами, а не на рисунке (лично для меня).
также существует таблица значений синуса, косинуса, тангенса и котангенса для некоторых углов (30°, 45°, 60°, 90°), тоже во вложении. таблицу нужно выучить обязательно.
ukrainian.
тригонометричні функції гострого кута прямокутного трикутника. sin, cos, tg, ctg.
у кожному прямокутному трикутнику є два гострих кута. для кожного з них можна знайти синус, косинус, тангенс та котангенс.
синус гострого кута пр. трикутника - це відношення (ділення) протилежного цьому куту катета до гіпотенузи.
косинус гострого кута пр. трикутника - це, відношення прилеглого цьому куту катета до гіпотенузи.
тангенс гострого кута пр. трикутника - це відношення протилежного цьому куту катета до прилеглого.
котангенс - це, навпаки, відношення прилеглого до цього кута катета до протилежного.
також існує таблиця значень синуса(sin), косинуса (cos), тангенса(tg) та котангенса (ctg) для деяких кутів (30°, 45°, 60°, 90°). таблицю потрібно вивчити.
таблицу можно легко выучить по принципу, данному на сайте
Задачи №1 - №3 решены Пользователем Fialka7 Умный
Добавлено решение задачи №4.
№1
Р = 36 см . Находим боковые стороны - они равны, значит а=(36-10)/2=13 см. Проводим высоту к основанию ВН. ВН²=13²-(10/2)²=144=12². S=BH*AC*1/2=12*10/2=60cм²
№2.
Р=24=а*4 а=6 см -сторона ромба. S=a²*sinA 18=36*sinA sinA=1/2 ∠А=30°, другой угол= 180-30=150°. ответ: 30°, 150°, 30°,150°.
№3
ищем сторону а. а=(128-48)/2=40см -боковая сторона. r=S/p где р-это полупериметр. р=128/2=64. Ищем S. Проведем высоту ВН.
ВН²=40²-24²=1024=32². BH=32 см, S=32*48*1/2=768 см². r=768/64=12 см. ответ: 12 см.
№4
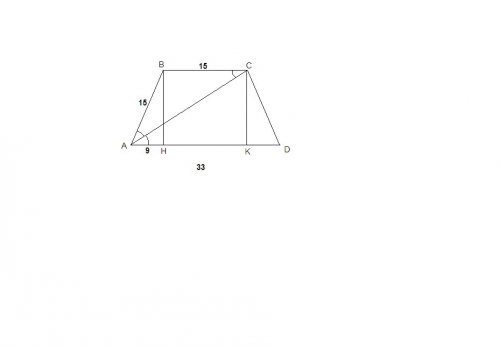
∠BAC = ∠DAC так как диагональ АС является биссектрисой угла А,
∠DAC = ∠BCA как накрест лежащие при пересечении параллельных прямых ВС и AD секущей АС, ⇒
∠ВАС = ∠ВСА, ⇒ ΔАВС равнобедренный, АВ = ВС = 15 см.
Отрезки, отсекаемые высотами равнобедренной трапеции на нижнем основании, равны полуразности оснований:
АН = (AD - BC) / 2 = (33 - 15)/2 = 9 см.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора:
ВН = √(АВ² - АН²) = √(15² - 9²) = √144 = 12 см
Sabcd = (AD + BC)/2 · BH = (33 + 15)/2 · 12 = 288 см²
Рассмотрим вертикальные углы , они равны по определению
2x = 114
x = 57 градусов
Смежный угол с углом x равен 180 - x = 123 гр
ответ : 123 и 57 градусов
Б )
Рассмотрим тот угол , что не учтён в 220 градусах
Поскольку сумма всех углов равна 360 , то угол равен 360 - 220 = 140 гр
Вертикальный с ним угол также равен 140 гр , а смежные с ними углы равны (360 - 140*2).2=40 градусов
ответ :140 и 40 градусов.
Если вы нашли ошибку или что-то не поняли , то напишите автору .
Powered by Plotofox .