***
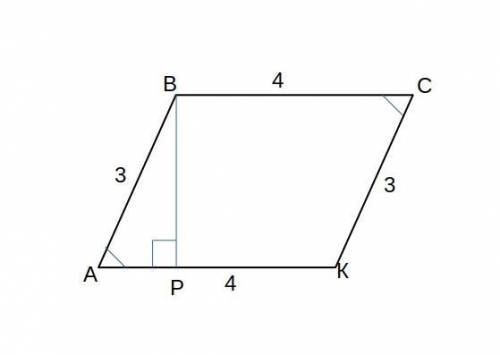
Дано:
АВСК параллелограмм
АВ = СК = 3 см
ВС = АК = 4 см
∠А = ∠С = 30°
задание можно решить
сделаем дополнительное построение
из вершины В проведем высоту ВР
ВР ⊥ АК
⇔
∠АРВ = 90°
⇔
треугольник АРВ прямоугольный
поскольку ∠А = 30°
а сторона, лежащая против угла в 30 градусов, равна половине длины гипотенузы треугольника
⇔
ВР = 1/2 · АВ = 1/2 · 3 = 1,5 см
площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота
S = ah = 4 · 1,5 = 6 см²
просто использовать формулу для нахождения площади параллелограмма через смежные стороны и углом между ними
S=a·b·sin30°
a = 3 см
b = 4 см
sin30° = 1/2
S = 3 · 4 · 1/2 = 12/2= 6 см²
ответ: площадь параллелограмма равна 6 см²
1) В четырехугольнике ABCD точки E и F — соответственно середины равных сторон AB и CD . Серединные перпендикуляр к стороне AD пересекает серединный перпендикуляр к стороне BC в точке P . Докажите, что серединный перпендикуляр, проведенный к отрезку EF проходит через точку P .
2) В четырехугольнике ABCD серединные перпендикуляры к сторонамAB и CD пересекаются на стороне AD . Известно, что \angle A = \angle D . Докажите, что в четырехугольнике диагонали равны.
3) В квадрате ABCD даны точки E и F соответственно на сторонах AB и BC ,причем \angle AED = \angle FED . Докажите равенство EF = AE + FC
так???!!!
BC = AB = 25
ΔАВН - прямоуг.=> cosB = BH/АВ = 14/25 = 0,56