Вравнобедренном треугольнике авс, где ав=вс, проведена биссиктриса см. найдите периметр авс, если ас=18, вм=24

👇

Увидеть ответ

Ответ:

misterwotblitz

05.12.2021

Пусть BC = x, тогда AM = BA - BM = x - 24

По свойству биссектрисы имеем:

$\frac{BC}{BM}=\frac{AC}{AM}$

Подставим все известные величины и найдём x:

$\frac{x}{24}=\frac{18}{x-24}\\ \\ x(x-24)=18\cdot 24\\ \\ x^2-24x-432=0\\\\ \sqrt{D}=\sqrt{576+1728}=\sqrt{2304}=48\\ \\ x_1=\frac{24-48}{2}=-12 \\ x_2=\frac{24+48}{2}=36$

x₁ не подходит по условию задачи, тогда BC = AB = 36

PΔABC = AB + BC + AC = 36 + 36 + 18 = 90

ответ: 90

4,8(2 оценок)

Ответ:

123qwerty0

05.12.2021

Гипотенуза делит противолежащую сторону на отрезки. пропорциональные прилежащим сторонам. Пусть АВ=ВС=х,

тогда АМ=х-24. Составим и решим пропорцию

ВС/АС=ВМ/АМ, х/18=24/х-24

х*(х-24)=18*24; х²-24х-18*24=0

х₁,₂=12±√(12²+18*24)=12±√(12²+12*36)=12±√(12*48)=12±24

х₁=36; х₂-12- не подходит по смыслу задачи.

Значит, ВС =АВ=36, а АС =18, тогда периметр равен 36+36+18=72+18=90

ответ периметр равен 90

4,4(81 оценок)

Открыть все ответы

Ответ:

mamarika2001

05.12.2021

а) Постройте плоскость, проходящую через точки K, L и М - для этого надо просто соединить эти точки.

б) Найдите угол между этой плоскостью и плоскостью основания АВС.
Продлим отрезки КМ и KL до пересечения с плоскостью АВС. Для этого достаточно продлить стороны АС и АВ.
Точки пресечения - это Д и Е.
Примем длину отрезка АК за 1.
Из треугольника АКД отрезок АД = 1 / tg 60 = 1 / √3.
Аналогично АЕ = 1 / tg 45 = = 1 / 1 = 1.
Угол ЕАД равен 60 градусов (по заданию).
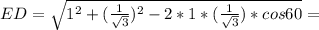
По теореме косинусов $ED= \sqrt{1^2+( \frac{1}{ \sqrt{3}} )^2-2*1*( \frac{1}{ \sqrt{3} } )*cos60}=$
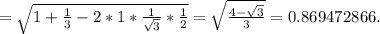
$= \sqrt{1+ \frac{1}{3} -2*1* \frac{1}{ \sqrt{3} }* \frac{1}{2}} = \sqrt{ \frac{4- \sqrt{3} }{3} } =0.869472866.
$
Находим гипотенузы в треугольниках АКД и АКЕ.
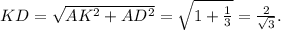
$KD= \sqrt{AK^2+AD^2} = \sqrt{1+ \frac{1}{3} } = \frac{2}{ \sqrt{3} } .$
КЕ = √(1²+1²) = √2 (острые углы по 45 градусов).
Теперь определены 3 стороны в треугольнике КЕД, угол наклона которого к плоскости АВС надо найти.
Для этого двугранный угол между основой и треугольником КДЕ надо рассечь плоскостью, перпендикулярной их линии пересечения ЕД.
Находим высоты в треугольниках АЕД и КЕД по формуле:
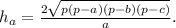
$h _{a} = \frac{2 \sqrt{p(p-a)(p-b)(p-c)} }{a} .$
АЕ ДЕ АД   p 2p S =
1   0.8694729    0.5773503   1.2234116   2.446823135     0.25
haе        hде      hад
0.5        0.57506   0.86603

КЕ    ДЕ   КД   p 2p S =
1.4142136 0.869473   1.154701   1.719194    3.43839   0.501492
hке    hде hкд
0.7092 1.15356   0.86861.
Отношение высот hде и  hде  - это косинус искомого угла:
cos α = 0.57506 / 1.15356 = 0.498510913.
ответ: α = 1.048916149 радиан = 60.09846842°.

4,7(87 оценок)

Ответ:

ИНТЕРНЕТ1111

05.12.2021

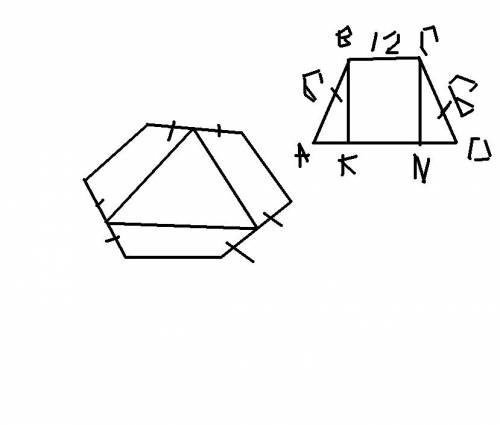
Рассмотрим трапецию ABCD, образованную стороной шестиугольника, двумя половина сторон шестиугольника и стороной построенного треугольника (то что этот четырехугольник трапеция следует из теоремы Фалеса и условия, что стороны треугольника соеденият середины шестиугольника)

AB=12 см, AD=BC=AB/2=6 см

проведем высоты BK и CN, тогда

BCNK - прямоугольник, треугольники AKB и DNC прямоугольные и равные

BC=KN=12 cм

угол АВС как внутренний угол правильного шестиугольника равен 120 градусов,отсюда

угол АВК равен 120-90=30 градусов, угол ВАК=90-30=60 градусов

Значит AK=AB*cos 60=AB/2=6/2=3 см

(или по свойству треугольника с углами 90,60, 30)

Значит сторона AD=3+12+3=18 см

Аналогично получаем что две другие стороны треугольника равны 18 см, т.е. полученный построением треугольник правильный

Искомая площадь треугольника как площадь правильного треугольника равна

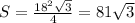$S=\frac{18^2\sqrt{3}}{4}=81\sqrt{3}$ кв.см