От всех сторон треугольника равноудалена точка пересечения его биссектрис, т.е. центр вписанной окружности.
Вершиной угла, под которым видна гипотенуза ( она - длинная сторона прямоугольного треугольника), является центр вписанной окружности, а его величина - разность между суммой углов треугольника и полусуммой его острых углов
∠АDВ=180°-0,5•(38°+52°)=135°
Заметим, что тупой угол, образованный биссектрисами острых углов прямоугольного треугольника всегда равен 135°, так как их сумма 90°, а полусумма -– 45°
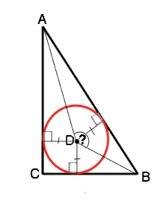
(AP-общая; ∠PAC=∠MAP; ∠ACP=∠PMA=90°)
AC=AM; △ACM равнобедренный; AS является биссектрисой и высотой; ∠ASC=90°
Аналогично △CBN равнобедренный; BT является биссектрисой и высотой; ∠BTC=90°
Угол между биссектрисами острых углов прямоугольного треугольника равен 45° (смежный 135°)
∠SOT =135°
Сумма углов четырехугольника равна 360°
Рассмотрим четырехугольник СSOT:
∠TCS + ∠CSO + ∠SOT + ∠OTC = 360°
∠TCS + 90° + 135° + 90° = 360° <=> ∠TCS = 45°