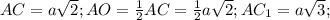
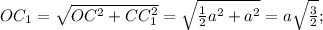
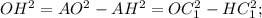
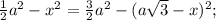
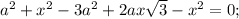
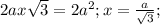
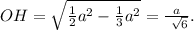
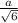
В данном нам равнобедренном треугольнике abc, высоты (они же биссектрисы и медианы), проведенные из равных углов (при основании) РАВНЫ. Проведем эти высоты AL и CK. Расстояния от точки d на основании АС - это отрезки dm и dn, параллельные высотам CK и AL соответственно. Прямоугольные треугольники АКС и ALC равны, так как АС - общая гипотенуза, катеты КС и AL - равны и равны углы LAC и КСА (так как AL и КС биссектрисы). Итак, в этих равных треугольниках линии dm и dn образуют подобные треугольники Adm и AKC, Cdn и CAL. Из их подобия имеем следующие отношения:
1)КС/dm=AC/Ad; 2)KC/dm=AC/dC. dm = 12-dn (дано) а Ad = АС-dC. Подставляем и имеем:
из 1): KC/12-dn = AC/AC-dC отсюда KC*(AC-dC) = AC*(12-dn) далее KC*AC - KC*dC = 12AC - AC*dn. Из 2): КС*dС = AC*dn. Из второго вставляем в первое и получаем:
КС*АС - АС*dn = 12АС - АС*dn или КС*АС = 12АС. И окончательно КС = 12, что и надо было найти.
В прямоугольнике все углы прямые, противоположные стороны равны и параллельны, а диагонали равны и точкой пересечения делятся пополам.
Пусть данный прямоугольник АВСD, точки К, М, Н, Т - соответственно середины АВ, ВС, СD, DА.
Соединим последовательно точки К,М,Н и Т
Треугольники КАТ, КВМ, МСН и НDТ прямоугольные, в каждом один катет равен половине меньшей стороны, другой - половине большей стороны. Следовательно, эти треугольники равны, отсюда равны их гипотенузы: КМ=МН=НТ=ТК.
КМНТ - четырехугольник, все стороны которого равны (признак ромба).
Кроме того: диагонали КН║ВС и МТ║АВ.
В прямоугольнике стороны пересекаются под прямым углом, ⇒
параллельные им диагонали ромба КН и МТ тоже пересекаются под прямым углом - признак ромба.
Четырехугольник КМНТ - ромб, и его вершинами являются середины сторон прямоугольника.