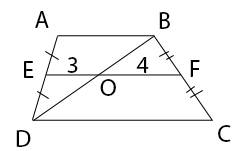
Дано: ABCD - трапеция
EF - средняя линия
EO = 3 см
OF = 4 см
Найти: AB
Решение.
1) Рассмотрим трапецию ABCD. Средняя линия EF параллельна основаниям AB и DC и делит стороны AD и BC трапеции пополам.
2) Рассмотрим треугольники EOD и ABD.
Углы EOD и ABD равны как соответственные при пересечении параллельных прямых EF и AB секущей BD.
Угол DBC общий. Следовательно, треугольник BOF подобен BDC.
3) Из подобия треугольников следует, что
AB / EO = AD / ED => AB = EO * AD / ED = EO * 2ED / ED = EO * 2 = 6 см
Пусть AB- х, тогда BC - 2x . По условию периметр=36. AB=CD BC=AD ( свойство параллелограмма) , тогда составим и решим уравнение: x+2x+x+2x=36
5x=36
x=36:5
х=7.2
Значит , AB=CD=7.2 , тогда, BC=7.2 умножить на 2 = 14.4, значит BC=AD=14.4
ответ : 7.2; 7.2; 14.4; 14.3