вот вам рисунок
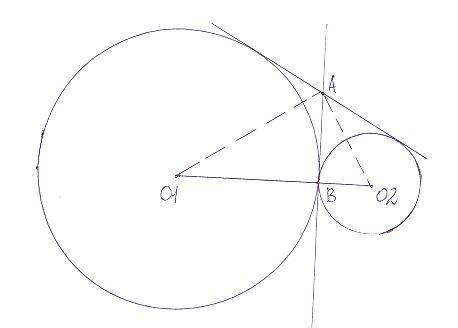
Решение очень простое - вся "хитрость" в том, что угол О1АО2 (между пунктирными прямыми) равен 90 градусам. Дело в том, что О1А и О2А - биссеткриссы смежных углов (почему биссектрисы, - это понятно? обоснуйте), а сумма смежных углов 180 градусов. Ну, сумма половин смежных углов (то есть сумма угла О1АВ и угла О2АВ) дает 90.
Таким образом, трегольник О1АО2 - прямоугольный, и АВ - высота к гипотенузе.
Дальше - очень полезное "заклинание" - хотя и очень простое.
Высота к гипотенузе делит прямоугольный треугольник на два, подобные ему - и между собой тоже, конечно.
Поэтому
О1B/АВ = АВ/О2В;
О1B = АВ^2/O2B = 6^2/4 = 9;
соединим концы хорды с центром окружности- получается равнобедренный треугольник Хорда АВ - это основание
радиусы - это боковые стороны
градусная мера угла при вершине треугольника равна дуге окружности -112 град
ДВА угла при основании треугольника равны каждый (180-112 ) / 2= 34 град
угол между радиусом и касательной 90 град - этот угол разделен хордой в свою очередь на два угла - один из которых (угол при основании треугольника) =34 град , а искомый
угол между этой хордой и касательной к окружности 90-34 =56 град
ответ 56 град
O₁∈b; O₁∈c; O₁∈d
Две различные прямые называются пересекающимися, если они имеют общую точку. Точка пересечения единственна: если две прямые имеют две общие точки, то они совпадают.
Прямые b и с пересекаются в точке O, они также пересекаются в точке O₁. Так как по условию прямые b и с не совпадают, точки O и O₁ совпадают.
Прямая d проходит через точку O. Прямые a, b, c, d проходят через одну точку.