Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
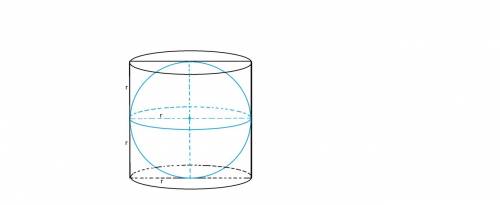
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
Верное решение зависит от правильного рисунка. Задача имеет два решения.
1). Луч ВD проходит между сторонами угла АВС. Тогда угол СВD=3 АВD. Сумма∠ АВD+∠CBD=36°, т.е. ∠ABD+3∠ABD=36°, ⇒ 4∠ABD=36°, откуда ∠АВD=36°:4=9°
2). Луч ВD проходит вне угла АВС. Тогда угол СВD=∠АВС+∠АВD=3∠ ABD. 3∠ABD=∠ABD+36°, откуда 2∠ABD=36°, ⇒ ∠АВD=36°:2=18°