2. Тр МКТ=трНКТ за кутами и общей стороной
3. кут Р = R, KS общая РКS~RKS
4. Кут S=куту R = 90°,EF - общаЯ
5. SMN= TMN, K = P = 90°,SP = KT, SM= MT
Объяснение:
15
Объяснение:
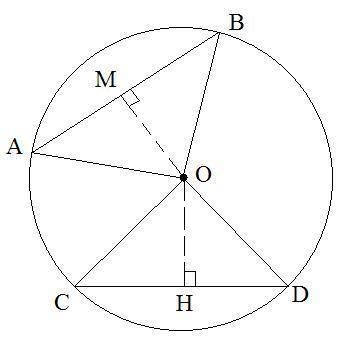
Треугольник AOB равнобедренный, так как AO=OB – как радиусы окружности. OM – расстояние от точки O до хорды AB, то есть,ОМ перпендикулярна АВ , получаем, что OM – высота и медиана (AM=MB) треугольника AOB. Так как AB=30, то AM=15. Найдем длину AO из прямоугольного треугольника AMO по теореме Пифагора:
АО= √ОМ^2+AM^2 = √8^2+15^2 = 17
Также это означает, что OC=OD=AO=17. Рассмотрим прямоугольный треугольник OCH (OH – расстояние от точки O до хорды CD) со стороной CH=CD:2=8. По теореме Пифагора находим длину OH:
OH = √OC^2-CH^2 = √17^2-8^2 = 15
ответ: 5:3
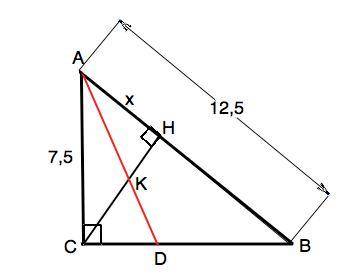
Объяснение: Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Обозначим точку пересечения биссектрисы АD и высоты СН буквой К. Тогда СК:КН=АС:АН.
В прямоугольном треугольнике катет есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
АС - катет, АН его проекция на гипотенузу. Примем АН=х ⇒ АС²=АВ•АН ⇒ 7,5²=12,5•х, откуда х=4,5
Искомое отношение СК:КН=7,5:4,5=5:3
MRT=TNS
Объяснение:
5)MRT=TNS
так как угол R и угол S равны
2) так как KT медиана треугольники будут равны