Дано: площадь полной поверхности конуса S = 45π см кв.
Развёртка боковой поверхности его - сектор с углом 60º.
Формула площади конуса: S = So + Sбок = πr² - πrL,
где r - радиус основания, L - образующая.
Используем вторую формулу площади боковой поверхности как сектора: πrL = πL²α/360°. Подставим α = 60° и сократим на πL:
r = L/6 или L = 6r.
Теперь значение образующей подставим в исходное уравнение, сокращённое на π: r² + r*6r = 45, получаем 7r² = 45 или r = √(45/7).
Находим высоту конуса H:
H = √(L² - r²) = √((6r)² - r²) = r√35 = √(45/7)*√35 = 15.
ответ: V= (1/3)SoH = (1/3)*(π*(45/7))*15 = π*(225/7).
ответ: V=48√3см³
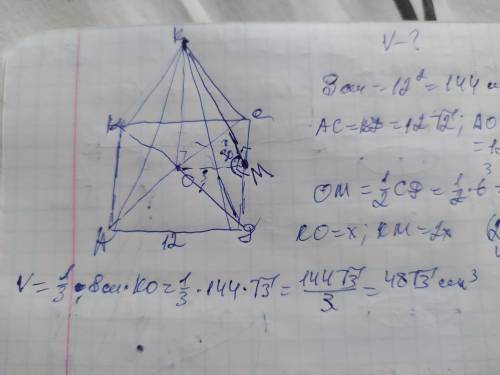
Объяснение: в основании правильной четырёхугольной пирамиды лежит квадрат поэтому все стороны основания равны. Обозначим вершины пирамиды АВСД с высотой КО и проведём две диагонали АС и ВД, которые делят основание на 4 равных равнобедренных прямоугольных треугольника в которых половины диагоналей являются катетами а сторона основания гипотенузой. Рассмотрим полученный ∆СОД. В нём проэкция апофемы ОМ на основание также является медианой, поскольку боковая грань пирамиды равнобедренная, поэтому медиана равна половине гипотенузы СД. ОМ=12/2=6см.
Рассмотрим ∆КМО. Он прямоугольный где КО и ОМ - катеты, а КМ- гипотенуза.
КО лежит напротив угла 30°, поэтому равен половине гипотенузы КМ. Пусть КО=х, тогда КМ=2х. Составим уравнение используя теорему Пифагора:
КМ²-КО²=ОМ²
(2х)²-х²=3²
4х²-х²=9
3х²=9
х²=9/3=3
х=√3; КО=√3см, тогда КМ=2√3см
Sосн=12²=144см²
Теперь найдём объем пирамиды зная её высоту и площадь основания по формуле:
V=⅓×Sосн×KO=⅓×144×√3=48√3см³
3х=120
х=120/3
х=40°
второй=2*40=80° все