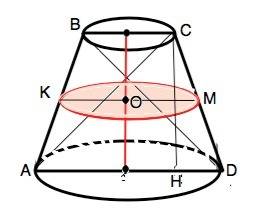
Осевое сечение усеченного конуса - равнобедренная трапеция АВСD с равными диагоналями. .
Взаимно перпендикулярные равные диагонали образуют с основаниями прямоугольные равнобедренные треугольники. Сумма высот этих треугольников=сумме их медиан=полусумме оснований. Отсюда: Если диагонали равнобедренной трапеции перпендикулярны, то её высота равна средней линии трапеции, т.е. полусумме оснований.
Сечение конуса, проведенное параллельно основанию, – круг.
Диаметр КМ сечения, проведенного через середину высоты осевого сечения параллельно основанию, равен средней линии такой трапеции, т.е. Н. Тогда радиус ОМ равен Н/2, а площадь
S=π•(H/2)²=π•Н²/4
1. Длины сторон
AB = √((-12-4)²+(-2-10)²) = 20
AC = √((-12+6)²+(-2+10)²) = 10
BC = √((4+6)²+(10+10)²) = 10√5
2. Биссектриса делит пересекаемую сторону на отрезки, пропорциональные прилегающим сторонам
BZ/CZ = AB/AC = 20/10 = 2
BZ = 2*CZ
BZ+CZ = 10√5
3*CZ = 10√5
CZ = 10/3√5
уравнение прямой СB в параметрической форме
x = -6+(4+6)t = -6 + 10t
y = 10
причём при t=0 получаем точку С, при t=1 - точку B
а при t = 1/3 - получим точку Z
x = -6 + 10*1/3 = - 8/3
y = 10
Z(-8/3;10)
и уравнение прямой AZ
(x+8/3)/(-12+8/3) = (y-10)/(-2-10)
или
-3x/28 + y/12 - 47/42 = 0