Площадь треугольника можно найти по формуле S=a•h:2 , где а- основание, h- высота, проведенная к нему.
Если у треугольников равны основания и высоты, то их площади равны.
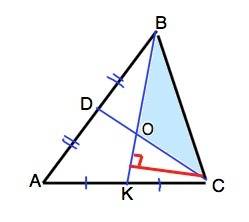
В треугольниках АВК и СВК основания АК=КС, высота из В – общая. Площади этих треугольников равны половине 0,5•SABC.
Следовательно, S ∆ ВСК=0,5 S ∆ АВС.
Рассмотрим ∆ КВС. Точка О делит ВК отношении ВО:ОК=2:1.
Это свойство точки пересечения медианы в задачах встречается нередко.
Высота для ∆ ВОС и КОС общая, поэтому площадь ∆ ВОС равна 2/3 площади ∆ КВС.
А т.к. S ∆ КВС=0,5 S ABC, то S ∆ ВОС=1/3 площади ∆ АВС.⇒
S ∆ АВС=3•S ∆ BOC=18 см²
Cм рисунок в приложении. Проведем высоты вы трапеции из вершин верхнего основания. Обозначим нижнее основание и боковые стороны х
Из прямоугольных треугольников находим катет
Катет равен гипотенузе х, умноженной на косинус 65°
(если бы 60°, то косинус 60° равен 0,5)
Тогда нижнее основание состоит их трех отрезков:
х·cos 65°+x+x·cos 65°=16 ⇒ x=16:(2cos 65°+`1)
cos 65°≈ 0,423
0,423х+х+0,423х=16
1,846 х=16
х≈8,67
Р≈8,67+8.67+8.67+16=42,01
Если все-таки 60° угол, то все гораздо проще:
0,5х+х+0,5х=16
2х=16
х=8
Р=8+8+8+16=40
Объяснение:
P=7,5+6+4,5(cm)
P=18(cm)
б)
P=8,1+7,9+12(cm)
P=28(cm)