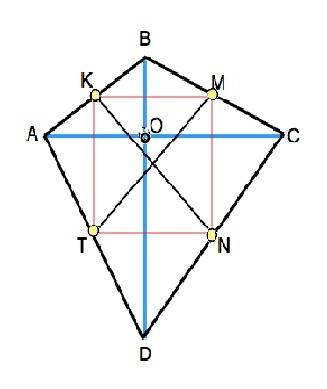
Пусть дан четырёхугольник АВСD. Точка К - середина АВ, т.М - середина ВС, N и Т - середины СD и DA соответсвенно. По условию КN=ТМ. Проведем диагонали АС и ВD. Соединим середины сторон треугольников АВС, ВСD, CDA и DAB. В треугольниках АВС и АDC средние линии параллельны и равны половине диагонали АС исходного четырехугольника.⇒ КМ параллельна и равна ТN. Аналогично доказывается КТ=МN. Противоположные стороны КМNТ параллельны и равны. КМNТ - параллелограмм с равными диагоналями ( КN=МТ по условию), т.е. КМNТ - прямоугольник. А раз стороны КМNТ пересекаются под прямым углом, то и диагонали четырехугольника АВСD, которым они параллельны, также пересекаются под прямым углом, ч.т.д.
1) S = 1/6
2) S = 1/2
3) S = 5/9
Объяснение:
Площадь треугольника можно вычислить по следующей формуле:
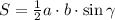
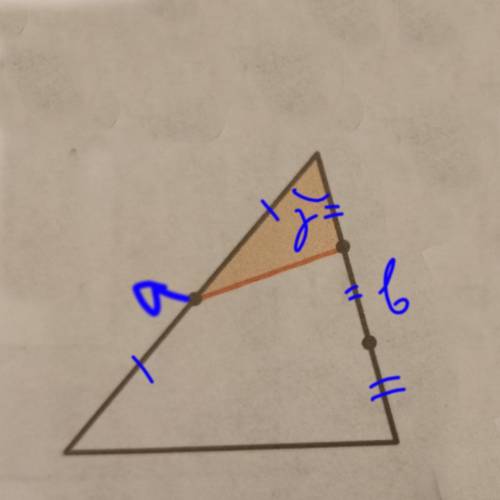
1) Обозначим площадь закрашенного ∆-ка S1 (см. рис.1)
Очевидно, т.к. точки делят стороны "единичного" ∆ка на равные отрезки, а угол 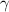 у единичного и у малого треугольника общий, то
у единичного и у малого треугольника общий, то
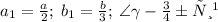
и площадь S1 равна
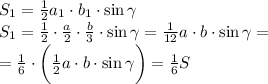
А т.к. 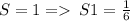
2) Пусть площадь закрашенной фигуры (а это - треугольник, см. рис.) равна S1.
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (обозначим их площади S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
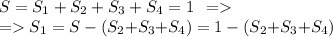
Треугольники 2, 3, 4 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
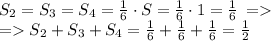
Соответственно, искомая площадь составляет
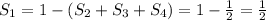
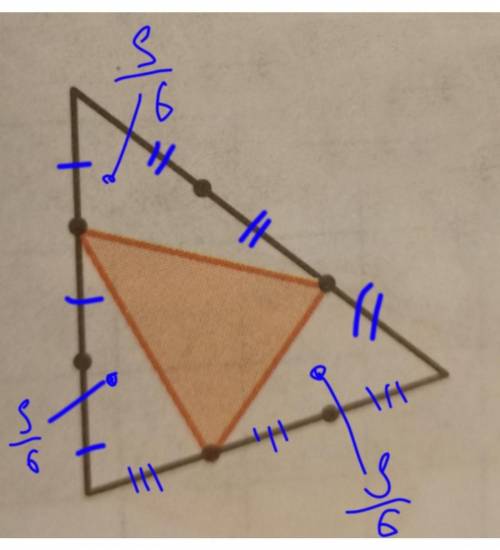
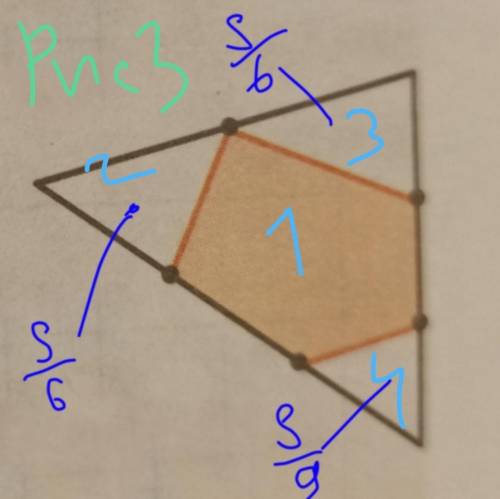
3) Пусть площадь закрашенной фигуры (а это - шестиугольник, см. рис.) равна S1
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (пусть их площади будут S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
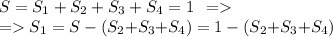
Площади треугольников 2, 3 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
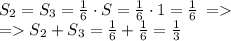
Но площадь треугольника 4 меньше: у него две стороны втрое меньше чем у исходного единичного, потому его площадь равна:
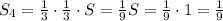
Следовательно, общая площадь незакрашенных частей равна:
А искомая площадь закрашенной фигуры S1 составляет
Треугольник АВС
АС - плоскость
АВ = 18
ВС = 24
Опускаем высоту ВД на плоскость АС
АK = х
KС = х+14
По теореме Пифагора
BK^2 = 18^2 - x^2 = 24^2 - (x+14)^2
324 - x^2 = 576 - x^2 - 28x - 196
28x = 56
x = 2
х+14 = 16
ответ: 2 и 16