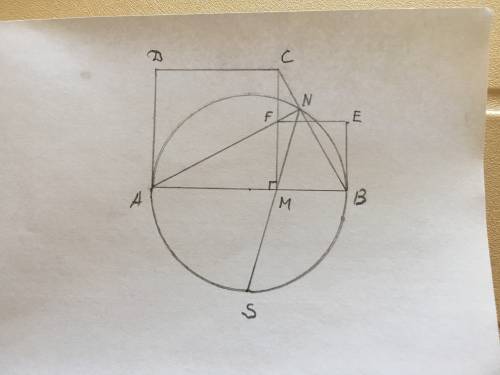
Из суммы углов треугольника в треугольнике АВС угол В=180°- ∠А-∠С=80°. По условию ВЕ=ВС ⇒ ∆ ВЕС равнобедренный, поэтому биссектриса ВН, принадлежащая прямой ВD, является его медианой и высотой. Прямоугольные Δ ВЕН =Δ ВСН, их углы при вершине В равны 80:2=40°, углы при основании ЕС равны по (180°-80°):2= 50°. Отсюда ∠НСD=60°-50°=10°. Угол СDH=180°- 90°-10°=80°. ∠НDA=180°-80°=100° ( смежный). В треугольнике СЕD точка Н - середина СЕ, ∠ЕНD=90° ⇒ HD - биссектриса угла D. ∠ВDЕ=80°, поэтому ∠АDE=∠АDH-∠EDH=100°-80°=20°.
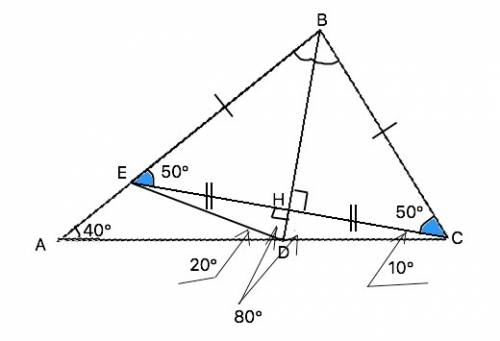
Обозначим AB=a, MB=MF=x, тогда AM=AC=a-x,
MO=MB·tg∠ABC=x(a-x)/a,
OF= MF-OM=x-x(a-x)/a=x²/a,
PB=AB·tg∠MAF=ax/(a-x).
Таким образом, BS=PB·MO/OF=(ax/(a-x))·(x(a-x)/a)·(a/x²)=a. Итак, видим, что длина BS не зависит от положения точки M на отрезке AB, т.е. точка S - искомая.