Відповідь:
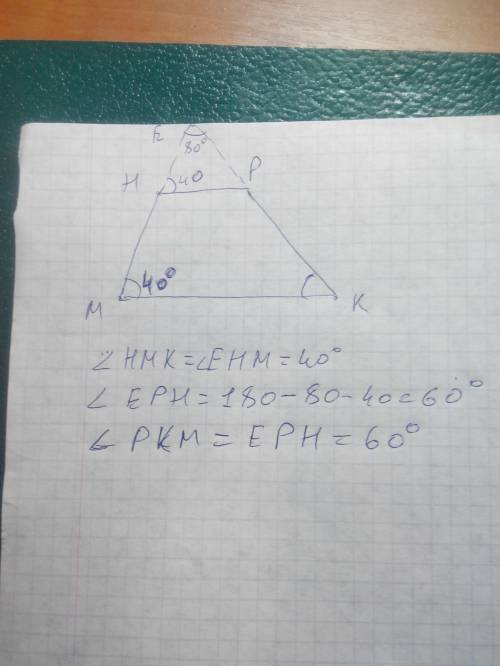
Задача вимагає знайти кути трикутника ВСD, враховуючи інформацію про кут BOD.
Оскільки ВО і ДО - радіуси кола, то ВОД - рівнобедрений трикутник, оскільки ВО = ДО (вони є радіусами кола). Тому кути ВОД і ДОВ також рівні.
Згідно з умовою, BOD = 70°. Тому ВОД = 70° (комплементарний кут до BOD).
Оскільки ВОД - рівнобедрений трикутник, то кути ВОД і ВДО також рівні. Тому ВДО = 70°.
За теоремою про суму кутів в трикутнику, сума всіх кутів трикутника ВСD дорівнює 180°. Отже, сума кутів ВСД = 180° - ВОД - ВДО.
Замінюючи значення, отримуємо: ВСД = 180° - 70° - 70° = 40°.
Отже, кути трикутника ВСД дорівнюють 40°, 70° і 70°.
ответ:прости могут быть ошибки.И надеюсь все верно
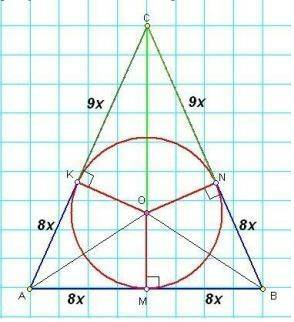
1) У рівнобедреному ΔАВС АС=ВС і СМ - висота, медіана та бісектриса,
ОМ - радіус вписаного кола, КА=АМ=NB=MB=8x, KC=CN=9x.
Площу трикутника можна знайти за формулою:
S=1/2AB*CM.
2) Розглянемо CMB - прямокутний.
По т.Піфагора знаходимо СМ=√(ВС²-ВМ²)=√((17х)²-(8х)²)=√(289х²-64х²)=
=√(225х²)=15х.
Оскільки центр вписаного кола - це точка перетину бісектрис, можна використовувати властивість бісектриси: b:c=b1:c1.
Використовуємо цю властивість для ΔСМВ та бісектриси ВО:
B:BM=CO:OM;
17x: 8x = CO: 16;
17:8 = CO: 16;
CO = 17 * 16 / 8 = 34 (см).
СМ = СО + ОМ = 34 +16 = 50 (см).
СМ = 15х = 50;
x = 50/15 = 10/3.
3) ABC: AB=16x=16*10/3=160/3 (см).
СМ = 50 см.
Знаходимо площу ΔАВС:
S=1/2*AB*CM=1/2*160/3*50=4000/3=1333 (см2).
Відповідь: 1333 см².
Объяснение: