По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
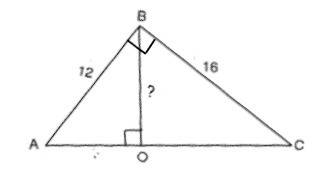
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
Духовные оды Ломоносова по праву признаются наиболее совершенными в художественном отношении поэтическими произведениями писателя. Медная крепость их стиля удивительно гармонирует с грандиозностью рисуемых образов. В дальнейшем не раз русская литература вновь и вновь обращалась к духовным проблемам, создавая высочайшие художественные творения, которые принесли ей мировую славу. В конце XVIII века дело Ломоносова продолжил Державин, а затем в поэзии XIX века натурфилософская поэзия Тютчева наследует традиции ломоносовских духовных од, особенно в создании картин ночного пейзажа. Конечно, классицизм с его строгим делением на стили и жанры безвозвратно ушел в оды, столь популярные среди писателей этого литературного направления, сменились другими стихотворными жанрами. Но сам накал духовного искания, выраженный в возвышенных художественных образах, связанных с библейской первоосновой, не мог исчерпать себя. В русской литературе он отразился в той ее пророческой ветви, которая дала нам незабываемых «Пророков» Пушкина и Лермонтова, навсегда связавших воедино в русской литературе имя Поэта с высокой миссией Пророка.
Объяснение: