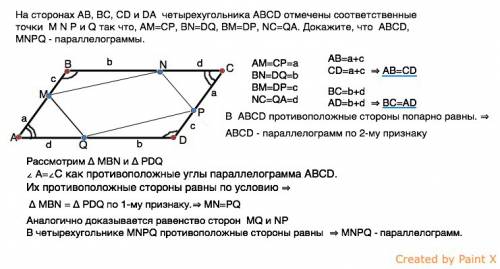
На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственные точки M N P и Q так что, AM=СP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD, MNPQ - параллелограммы.
***
Обозначим равные отрезки одинаковыми буквами:
АМ=СР=а
BN=DQ=b
BM=DP=c
NC=QA=d
АВ=а+с
СD=a+c ⇒ AB=CD
BC=b+d
AD=b+d ⇒ BC=AD
В четырехугольнике АВСD противоположные стороны попарно равны. ⇒
АВСD - параллелограмм ( 2-й признак)
–––––––––––––––––––––
Рассмотрим ∆ MBN и ∆ PDQ
∠ А=∠С как противоположные углы параллелограмма АВСD.
Содержащие эти углы стороны равны по условию ⇒
∆ MBN = ∆ PDQ по 1-му признаку.⇒ MN=PQ
Аналогично доказывается равенство сторон MQ и NP
В четырехугольнике MNРQ противоположные стороны равны ⇒ MNРQ - параллелограмм.
З умови задачі нам відомо, що кут при вершині одного трикутнику, дорівнює куту при вершині іншого. Також ми знаємо, що ці трикутники рівнобедрені. Р одного трикутника дорівнює 30 см, тоді Р іншого трикутника, також дорівнює 30 см. Основа відноситься к бічній стороні як 1 : 2. складемо рівняння.
2х+х+2х (бічні сторони рівні) = 30 см
5х = 30 см
х = 6 см
Звідси виходить, що бічні сторони (2х) дорівнюють 12 см (2×6)
Відповідь: основа (а) = 6 см, бічні сторони (b,c) = 12 см.
P.S Прости если будет не правельно