4 см
Объяснение:
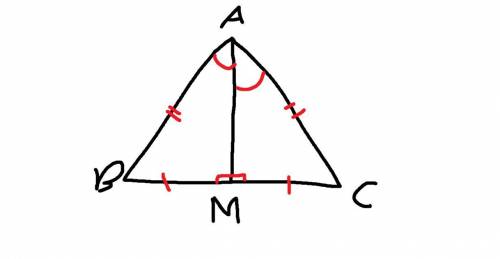
Так как высота АМ , проведённая из вершины равнобедренного треугольника, является медианой и биссектрисой, то углы ∠ВАМ и ∠САМ равны, а так как ∠ ВАС = 90 °, то они равны 45°.
Известно, что сумма углов треугольника равна 180°, значит в ΔСАМ ∠АСМ = 180° - 90° - 45° = 45°, а следовательно ΔСАМ - равнобедренный, что означает равенство сторон АМ и СМ
Высота АМ (медиана и биссектриса) делит сторону ВС на 2 равные части, а так как ВС = 8, то значит, что МС = 1/2 * 8 = 4, а так как МС = АМ, то и АМ = 4
Угол АСВ-90° (дано). Призма прямая > все ее боковые грани - прямоугольники. Катет АС треугольника АВС прилежит углу 60°, > гипотенуза АВ-АС:сos60°-а:0,5%32а. Катет ВС-АB.sin60°-2a-V3/2-аv3. В1С1 перпендикулярен плоскости АА1С1C, следовательно, перпендикулярен А1С1, а СС1-проекция наклонной ВIС. По условию B1CC1-45°. Значит, В1С -биссектриса прямого угла, угол С1В1С-45°, и Д ВІС1С - равнобедренный, поэтому высота призмы СС1-B1C1-Bс-av3 Формула площади боковой поверхности призмы S-P-H (произведение периметра основания и высоты призмы). S-fa+2atav3)-av3-а*-(3+V3)