пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.
118°, 118°, 62°, 62°
Объяснение:
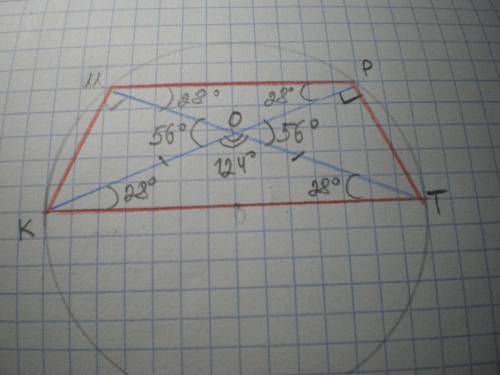
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
ответ: четырехугольник ABCD является ромбом.