величина отрезков АН,КД=16/2=8СМ
AД=8*2+х
АД+ВС=16+х+х=38см
2х=22см
х=11 (см)-меньшое основание
х+16=27 (см)-большое основание
Сумма внешних углов правильного многоугольника всегда равна 360 градусов Сумма внутренних углов = 360 + 720 = 1080 градусов По формуле 180(n-2) = 1080 (n обозначает кол-во сторон првильного многоугольника) находим, что n = 8
длина стороны правильного многоугольника = периметр / кол-во сторон = 144/8 = 18 см
В этом решении n они находят:
По формуле 180(n-2) = 1080
но ведь эта формула, подходит для произвольного многоугольника, а для правильного нужно 180(n-2)/n
но когда я решаю по правильной формуле, ответ не получается 18, почему?? почему используется в решении другая формула?
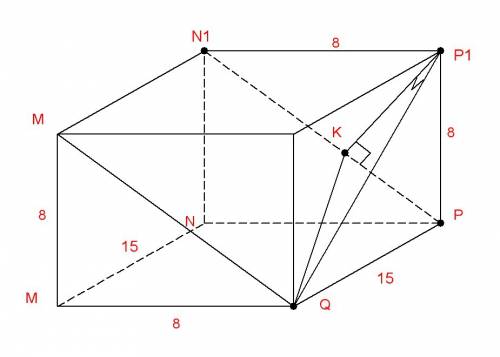

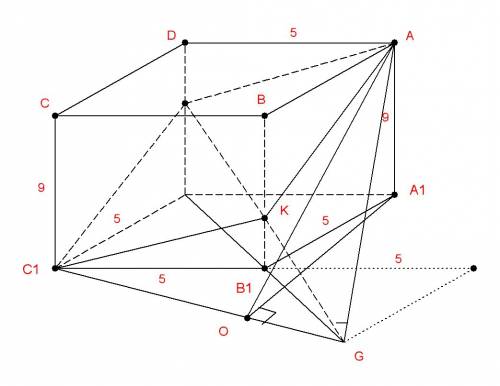
Опустим из вершин меньшего основания перпендикуляры к большему. Трапеция равнобедренная, значит, большее основание равно меньшему основанию плюс два равных отрезка при углах 60°.
Отрезки находим из прямоугоных треугольников, в которых один из углов по условию задачи 60°, второй по построению 90°, третий, соответственно, 30°.
Известно, что катет, противолежащий углу 30°, равен половине гипотенузы.
Величина отрезков АН и КД равна 16:2=8 см
АД=8*2+х
АД+ВС=16+х+х=38см
2х=22см
х=11 см-это меньшее основание
х+16=27 см- это большее основание.
ответ: АД=27 см,ВС=11 см